题目内容
已知f(x)=(4a-3)x-2a,a∈[0,1],若f(x)≤2恒成立,则x的取值范围是 .
【答案】分析:f(x)≤2,整理可得关于a的一次函数,利用一次函数的性质可得不等式组,解出即可.
解答:解:f(x)≤2,即(4a-3)x-2a≤2,亦即(4x-2)a-3x-2≤0,
由题意可得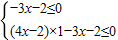 ,解得-
,解得-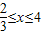 ,
,
故答案为:[- ,4].
,4].
点评:本题考查一次函数的性质、函数恒成立问题,属中档题.
解答:解:f(x)≤2,即(4a-3)x-2a≤2,亦即(4x-2)a-3x-2≤0,
由题意可得
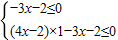 ,解得-
,解得-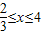 ,
,故答案为:[-
 ,4].
,4].点评:本题考查一次函数的性质、函数恒成立问题,属中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目

