题目内容
下列命题中假命题 是
- A.若
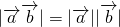 ,则
,则 ∥
∥
- B.
 在
在 方向上的投影为
方向上的投影为
- C.若△ABC中,a=5,b=8,c=7,则

- D.若非零向量
 、
、 满足|
满足| +
+ |=|
|=| -
- |,则
|,则 ⊥
⊥
C
分析:A:根据向量的数量积运算,可得cosθ=±1,所以 ∥
∥ .B:根据向量的投影的计算公式可得:
.B:根据向量的投影的计算公式可得: 在
在 方向上的投影为
方向上的投影为 .C:由余弦定理可得cos∠C=
.C:由余弦定理可得cos∠C= ,所以∠C为锐角,所以
,所以∠C为锐角,所以 错误.D:对|
错误.D:对| +
+ |=|
|=| -
- |平方可得
|平方可得 ,所以
,所以 ⊥
⊥ .
.
解答:A:若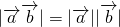 ,即
,即 ,所以cosθ=±1,所以
,所以cosθ=±1,所以 ∥
∥ .所以A正确.
.所以A正确.
B:根据向量的投影的计算公式可得: 在
在 方向上的投影为
方向上的投影为 .
.
C:若△ABC中,a=5,b=8,c=7,则由余弦定理可得cos∠C= ,所以∠C为锐角,所以
,所以∠C为锐角,所以 错误.
错误.
D:若有| +
+ |=|
|=| -
- |,则
|,则 =
= 即
即 ,所以
,所以 ⊥
⊥ .
.
故选C.
点评:解决此类问题的关键是熟练掌握向量的运算法则与向量的数量积运算,以及向量的投影等有关运算.
分析:A:根据向量的数量积运算,可得cosθ=±1,所以
 ∥
∥ .B:根据向量的投影的计算公式可得:
.B:根据向量的投影的计算公式可得: 在
在 方向上的投影为
方向上的投影为 .C:由余弦定理可得cos∠C=
.C:由余弦定理可得cos∠C= ,所以∠C为锐角,所以
,所以∠C为锐角,所以 错误.D:对|
错误.D:对| +
+ |=|
|=| -
- |平方可得
|平方可得 ,所以
,所以 ⊥
⊥ .
.解答:A:若
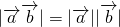 ,即
,即 ,所以cosθ=±1,所以
,所以cosθ=±1,所以 ∥
∥ .所以A正确.
.所以A正确.B:根据向量的投影的计算公式可得:
 在
在 方向上的投影为
方向上的投影为 .
.C:若△ABC中,a=5,b=8,c=7,则由余弦定理可得cos∠C=
 ,所以∠C为锐角,所以
,所以∠C为锐角,所以 错误.
错误.D:若有|
 +
+ |=|
|=| -
- |,则
|,则 =
= 即
即 ,所以
,所以 ⊥
⊥ .
.故选C.
点评:解决此类问题的关键是熟练掌握向量的运算法则与向量的数量积运算,以及向量的投影等有关运算.

练习册系列答案
相关题目
 ,那么下列命题中假命题是( )
,那么下列命题中假命题是( )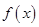 既不是奇函数,也不是偶函数 B.
既不是奇函数,也不是偶函数 B.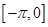 上恰有一个零点
上恰有一个零点 上是增函数
上是增函数 的双曲线的两条渐近线互相垂直
的双曲线的两条渐近线互相垂直 垂直的直线方程是2x+y-3=0
垂直的直线方程是2x+y-3=0 的两条准线之间的距离为
的两条准线之间的距离为