题目内容
若{an}为等差数列,a3=4,a8=19,则数列{an}的前10项和为
- A.230
- B.140
- C.115
- D.95
C
分析:分别利用等差数列的通项公式化简已知的两个等式,得到①和②,联立即可求出首项和公差,然后利用求出的首项和公差,根据公差数列的前n项和的公式即可求出数列前10项的和.
解答:a3=a1+2d=4①,a8=a1+7d=19②,
②-①得5d=15,
解得d=3,
把d=3代入①求得a1=-2,
所以S10=10×(-2)+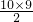 ×3=115
×3=115
故选C.
点评:此题考查学生灵活运用等差数列的通项公式及前n项和的公式化简求值,是一道基础题.
分析:分别利用等差数列的通项公式化简已知的两个等式,得到①和②,联立即可求出首项和公差,然后利用求出的首项和公差,根据公差数列的前n项和的公式即可求出数列前10项的和.
解答:a3=a1+2d=4①,a8=a1+7d=19②,
②-①得5d=15,
解得d=3,
把d=3代入①求得a1=-2,
所以S10=10×(-2)+
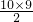 ×3=115
×3=115故选C.
点评:此题考查学生灵活运用等差数列的通项公式及前n项和的公式化简求值,是一道基础题.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目