题目内容
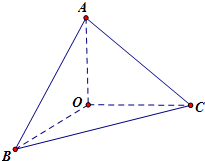 如图所示,三棱锥O-ABC中,OA=OB=OC=2,且,OA、OB、OC两两垂直(每两条都垂直).
如图所示,三棱锥O-ABC中,OA=OB=OC=2,且,OA、OB、OC两两垂直(每两条都垂直).(1)求三棱锥O-ABC的体积;
(2)求三棱锥O-ABC的高(O点到平面ABC的距离);
(3)求三棱锥O-ABC外接球的表面积(三棱锥O-ABC四个顶点都在球面上).
分析:(1)转化三棱锥O-ABC的体积的为三棱锥A-OBC的体积,直接求三棱锥O-ABC的体积;
(2)利用体积公式直接求三棱锥O-ABC的高(O点到平面ABC的距离);
(3)扩展三棱锥为长方体,求出三棱锥O-ABC外接球的半径,然后求解其表面积(三棱锥O-ABC四个顶点都在球面上).
(2)利用体积公式直接求三棱锥O-ABC的高(O点到平面ABC的距离);
(3)扩展三棱锥为长方体,求出三棱锥O-ABC外接球的半径,然后求解其表面积(三棱锥O-ABC四个顶点都在球面上).
解答: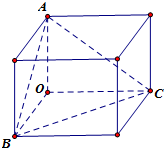 解(1)VO-ABC=VA-OBC=
解(1)VO-ABC=VA-OBC=
S△OBC•OA=
…4′
(2)设三棱锥O-ABC高为h,
由已知可得AB=BC=CA=2
…5′
∴S△ABC=2
…7′
由VO-ABC=
S△ABC•h=
得h=
∴三棱锥O-ABC的高为
…9′
(3)以OA、OB、OC的棱将三棱锥O-ABC补为一个长方体如图所示,
则三棱锥O-ABC的外接球就是该长方体的外接球,…10′
外接球直径2R=2
,即R=
…13′
球的表面积为S =4πR2=12π…14′
 解(1)VO-ABC=VA-OBC=
解(1)VO-ABC=VA-OBC=| 1 |
| 3 |
| 4 |
| 3 |
(2)设三棱锥O-ABC高为h,
由已知可得AB=BC=CA=2
| 2 |
∴S△ABC=2
| 3 |
由VO-ABC=
| 1 |
| 3 |
| 4 |
| 3 |
得h=
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
(3)以OA、OB、OC的棱将三棱锥O-ABC补为一个长方体如图所示,
则三棱锥O-ABC的外接球就是该长方体的外接球,…10′
外接球直径2R=2
| 3 |
| 3 |
球的表面积为S =4πR2=12π…14′
点评:本题考查几何体的体积的应用,球的内接多面体的应用,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
如图所示是三棱锥D-ABC的三视图,点O在三个视图中都是所在边的中点,则异面直线DO和AB所成角的余弦值等于( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知正方形ABCD的边长为2
已知正方形ABCD的边长为2
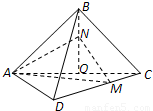 已知正方形ABCD的边长为2
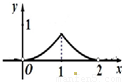
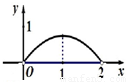
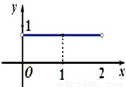
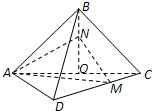
已知正方形ABCD的边长为2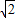 ,将△ABC沿对角线AC折起,使平面ABC⊥平面ACD,得到如图所示的三棱锥B-ACD.若O为AC边的中点,M,N分别为线段DC,BO上的动点(不包括端点),且BN=CM.设BN=x,则三棱锥N-AMC的体积y=f(x)的函数图象大致是( )
,将△ABC沿对角线AC折起,使平面ABC⊥平面ACD,得到如图所示的三棱锥B-ACD.若O为AC边的中点,M,N分别为线段DC,BO上的动点(不包括端点),且BN=CM.设BN=x,则三棱锥N-AMC的体积y=f(x)的函数图象大致是( )