题目内容
已知双曲线 (a>0,b>0)的左、右焦点分别为F1、F2,记
(a>0,b>0)的左、右焦点分别为F1、F2,记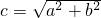 ,P是直线
,P是直线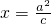 上一点,且PF1⊥PF2,|PF1|•|PF2|=4ab,则双曲线的离心率是
上一点,且PF1⊥PF2,|PF1|•|PF2|=4ab,则双曲线的离心率是
- A.

- B.

- C.2
- D.3
B
分析:依题意,△PF1F2为直角三角形,利用勾股定理与双曲线的定义,结合|PF1|•|PF2|=4ab,即可求得双曲线的离心率.
解答:∵PF1⊥PF2,
∴△PF1F2为直角三角形,
∴ +
+ =
= =4c2,①
=4c2,①
又 =
= +
+ -2
-2 =4a2,②
=4a2,②
①-②得:2 =4c2-4a2=4b2,③
=4c2-4a2=4b2,③
又|PF1|•|PF2|=4ab,④
 得:b=2a,
得:b=2a,
∴c2=a2+b2=5a2,
∴双曲线的离心率e= .
.
故选B.
点评:本题考查双曲线的简单性质,通过方程组求得b=2a是关键,考查通过分析与转化解决问题的能力,属于中档题.
分析:依题意,△PF1F2为直角三角形,利用勾股定理与双曲线的定义,结合|PF1|•|PF2|=4ab,即可求得双曲线的离心率.
解答:∵PF1⊥PF2,
∴△PF1F2为直角三角形,
∴
 +
+ =
= =4c2,①
=4c2,①又
 =
= +
+ -2
-2 =4a2,②
=4a2,②①-②得:2
 =4c2-4a2=4b2,③
=4c2-4a2=4b2,③又|PF1|•|PF2|=4ab,④
 得:b=2a,
得:b=2a,∴c2=a2+b2=5a2,
∴双曲线的离心率e=
 .
.故选B.
点评:本题考查双曲线的简单性质,通过方程组求得b=2a是关键,考查通过分析与转化解决问题的能力,属于中档题.

练习册系列答案
相关题目











 (a>0,b>0)的左右焦点分别为F1、 F2 ,P 是双曲线上的一点,且P F1⊥P F2,
(a>0,b>0)的左右焦点分别为F1、 F2 ,P 是双曲线上的一点,且P F1⊥P F2,  的面积为2 ab,则双曲线的离心率 e=________.
的面积为2 ab,则双曲线的离心率 e=________. (a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( )
(a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( ) (B)
(B) (C)
(C) (D)
(D)