题目内容
当x∈(1,2)时,不等式x-1<logax恒成立,求a的取值范围.
解:∵x-1<logax在(1,2)上恒成立
∴logax-x+1>0在(1,2)上恒成立
令f(x)=logax-x+1
f′(x)=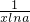 -1
-1
令f′(x)=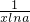 -1=0解得x=
-1=0解得x=
当0<a<1时,f′(x)<0
则函数f(x)在(1,2)上单调递减,则loga2-2+1≥0即1<a≤2,此时a无解
当1<a≤ 时
时 ≥2,f′(x)>0
≥2,f′(x)>0
则函数f(x)在(1,2)上单调递增,则loga1-1+1≥0,此时1<a≤
当 <a<e时1<
<a<e时1< <2,
<2,
则函数f(x)在(1, )上单调递增,在(
)上单调递增,在( ,2)上单调递减,loga2-2+1≥0即1<a≤2,此时
,2)上单调递减,loga2-2+1≥0即1<a≤2,此时 <a≤2
<a≤2
当a≥e时0< ≤1,f′(x)<0
≤1,f′(x)<0
则函数f(x)在(1,2)上单调递减,则loga2-2+1≥0即1<a≤2,此时a无解
综上所述:1<a≤2
分析:作差构造新函数f(x)=logax-x+1,利用导数研究函数最值证明不等式恒成立,从而求出a的取值范围.
点评:本题考查的知识点是对数函数的单调性与特殊点,以及函数恒成立问题,同时考查了分类讨论的数学思想,属于中档题.
∴logax-x+1>0在(1,2)上恒成立
令f(x)=logax-x+1
f′(x)=
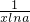 -1
-1令f′(x)=
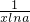 -1=0解得x=
-1=0解得x=
当0<a<1时,f′(x)<0
则函数f(x)在(1,2)上单调递减,则loga2-2+1≥0即1<a≤2,此时a无解
当1<a≤
 时
时 ≥2,f′(x)>0
≥2,f′(x)>0则函数f(x)在(1,2)上单调递增,则loga1-1+1≥0,此时1<a≤

当
 <a<e时1<
<a<e时1< <2,
<2,则函数f(x)在(1,
 )上单调递增,在(
)上单调递增,在( ,2)上单调递减,loga2-2+1≥0即1<a≤2,此时
,2)上单调递减,loga2-2+1≥0即1<a≤2,此时 <a≤2
<a≤2当a≥e时0<
 ≤1,f′(x)<0
≤1,f′(x)<0则函数f(x)在(1,2)上单调递减,则loga2-2+1≥0即1<a≤2,此时a无解
综上所述:1<a≤2
分析:作差构造新函数f(x)=logax-x+1,利用导数研究函数最值证明不等式恒成立,从而求出a的取值范围.
点评:本题考查的知识点是对数函数的单调性与特殊点,以及函数恒成立问题,同时考查了分类讨论的数学思想,属于中档题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
在R上可导的函数f(x)=
x3+
ax2+2bx+c,当x∈(0,1)时取得极大值.当x∈(1,2)时取得极小值,则
的取值范围是( )
| 1 |
| 3 |
| 1 |
| 2 |
| b-2 |
| a-1 |
A、(
| ||||
B、(
| ||||
C、(-
| ||||
D、(
|