题目内容
(本小题满分12分)
 如图,平面ABCD⊥平面PAD,△APD是直角三角形,∠APD=90°四边形ABCD是直角梯形,其中BC
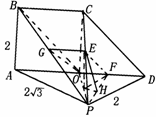
如图,平面ABCD⊥平面PAD,△APD是直角三角形,∠APD=90°四边形ABCD是直角梯形,其中BC![]() AD,∠BAD=90°,AD=2 BC,且BC=PD,O是AD的中点,E,F是PC,OD的中点.
AD,∠BAD=90°,AD=2 BC,且BC=PD,O是AD的中点,E,F是PC,OD的中点.
(Ⅰ)求证:EF![]() 平面PBO;
平面PBO;
(Ⅱ)证明:PF⊥平面ABCD.
(本小题满分12分)
解:(Ⅰ)取BP中点G,连EG,由E为PC中点
故EG![]()
![]() 又F为OD中点
又F为OD中点
 ∴OF=
∴OF=![]()
∴EF![]() OF,故四边形OFEG为平行四边形…………(3分)
OF,故四边形OFEG为平行四边形…………(3分)
∴EF∥GO 则EF∥面PBO…………………………(5分)
(Ⅱ) ∵四边形ABCD是直角梯形,∠BAD=90°
∴AB⊥AD
又平面ABCD⊥平面PAD
∴AB⊥平面PAD
又PF![]() 平面PAD
平面PAD
∴AB⊥PF……………………………………………………………………………………(8分)
在Rt△APD中,O为AE的中点,BC=PD,AD=2BC
∴PO=OD=PD
即△OPD为正三角形
又F为OD的中点
∴PF⊥OD…………………………………………………………………………………(11分)
∴PF⊥平面ABCD…………………………………………………………………………(12分)

练习册系列答案
相关题目