题目内容
已知椭圆C1的方程为(1)求双曲线C2的方程;
(2)若直线l:y=kx+![]() 与椭圆C1及双曲线C2都恒有两个不同的交点,且l与C2的两个交点A和B满足
与椭圆C1及双曲线C2都恒有两个不同的交点,且l与C2的两个交点A和B满足![]() ·
·![]() <6(其中O为原点),求k的取值范围.
<6(其中O为原点),求k的取值范围.
解:(1)设双曲线C2的方程为![]() -
-![]() =1,则a2=4-1=3,b2=4-3=1.
=1,则a2=4-1=3,b2=4-3=1.
故C2的方程为![]() -y2=1.
-y2=1.
(2)将y=kx+![]() 代入
代入![]() +y2=1,得
+y2=1,得
(1+4k2)x2+8![]() kx+4=0.
kx+4=0.
由直线l与椭圆C1恒有两个不同的交点得
Δ1=(8![]() k)2-4(1+4k2)×4>0,
k)2-4(1+4k2)×4>0,
即k2>![]() . ①
. ①
将y=kx+![]() 代入
代入![]() -y2=1,得(1-3k2)x2-6
-y2=1,得(1-3k2)x2-6![]() kx-9=0.
kx-9=0.
由直线l与C2有两个不同的交点得
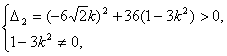
即k2<1且k2≠![]() . ②
. ②
设A(x1,y2)、B(x2,y2),则x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
由![]() ·
·![]() <6,得x1x2+y1y2<6,
<6,得x1x2+y1y2<6,
而x1x2+y1y2=x1x2+(kx1+![]() )(kx2+
)(kx2+![]() )
)
=(1+k2)x1x2+![]() k(x1+x2)+2=
k(x1+x2)+2=![]() ,
,
于是![]() <6,即
<6,即![]() >0.
>0.
∴k2>![]() 或k2<
或k2<![]() . ③
. ③
由①②③得![]() <k2<
<k2<![]() 或
或![]() <k2<1.
<k2<1.
故k的取值范围为(-1,-![]() )∪(-
)∪(-![]() ,-
,-![]() )∪(
)∪(![]() ,
,![]() )∪(
)∪(![]() ,1).
,1).

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目