题目内容
已知一曲线是与两个定点O(0,0)、A(a,0)(a≠0)距离之比为k(k≠1)的点的轨迹,求此曲线的方程,并判断曲线的形状.
解:设M(x,y)是曲线上任意一点,则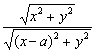
=k,化简得(k2－1)x2＋(k2－1)y2－2k2ax＋k
又∵k＞0且k≠1,∴k2－1≠0.
∵x2＋y2＋
x＋
=0.
∵D2＋E2－
－
=
＞0,
∴所求曲线方程为x2＋y2＋
x＋
=0.曲线是一个圆.
练习册系列答案
相关题目
题目内容
已知一曲线是与两个定点O(0,0)、A(a,0)(a≠0)距离之比为k(k≠1)的点的轨迹,求此曲线的方程,并判断曲线的形状.
解:设M(x,y)是曲线上任意一点,则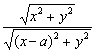=k,化简得(k2－1)x2＋(k2－1)y2－2k2ax＋k
又∵k＞0且k≠1,∴k2－1≠0.
∵x2＋y2＋x＋=0.
∵D2＋E2－－=＞0,
∴所求曲线方程为x2＋y2＋x＋=0.曲线是一个圆.
·
＝0，直线AE与BF交于点P(x0，y0)，求证：
为定值；
和点E的直线是曲线Q的一条切线．
·
＝
·
(或|
=0，直线AE与BF交于点P(x0，y0)，求证：
为定值;
(或
)，若存在，求出此时点E的坐标；若不存在，说明理由.