题目内容
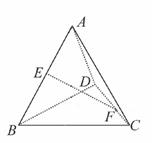
已知空间正四面体A-BCD，则异面直线AB和CD所成角的度数为 ．
【答案】分析：取AB中点E，连接CE、DE．根据等边三角形的中线也是高，得CE⊥AB且DE⊥AB，所以AB⊥平面CDE，从而有AB、CD互相垂直，得到它们所成的角为90°．
解答：解：
取AB中点E，连接CE、DE
∵△ABC中，CA=CB，E为AB的中点，∴CE⊥AB
同理可得DE⊥AB
∵CE、DE是平面CDE内的相交直线，∴∵CD⊆平面CDE，AB⊥CD
即异面直线AB和CD所成角的度数是90°
故答案为：90
点评：本题求正四面体相对的棱所成角，着重考查了线面垂直的判定与性质，异面直线所成角的求法等知识，属于基础题．
解答：解：
取AB中点E，连接CE、DE∵△ABC中，CA=CB，E为AB的中点，∴CE⊥AB
同理可得DE⊥AB
∵CE、DE是平面CDE内的相交直线，∴∵CD⊆平面CDE，AB⊥CD
即异面直线AB和CD所成角的度数是90°
故答案为：90
点评：本题求正四面体相对的棱所成角，着重考查了线面垂直的判定与性质，异面直线所成角的求法等知识，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
