题目内容
已知定义在R上的函数f(x)满足f(1)=1,f(1-x)=1-f(x),2f(x)=f(4x),且当0≤x1<x2≤1时,f(x1)≤f(x2),则f(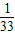 )等于( )
)等于( )A.

B.

C.
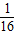
D.
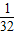
【答案】分析:先求出f( ),然后根据条件求出f
),然后根据条件求出f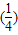 ,
,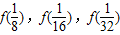 ,最后根据函数的单调性,以及两边夹的性质可求出所求.
,最后根据函数的单调性,以及两边夹的性质可求出所求.
解答:解:∵f(1)=1,f(1-x)=1-f(x)
令x= 得f(
得f( )+f(
)+f( )=1即f(
)=1即f( )=
)=
∵2f(x)=f(4x)
∴f(x)= f(4x)
f(4x)
在f(x)= f(4x)中,令x=
f(4x)中,令x= 可得f(
可得f( )=
)=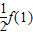 =
=
在f(1-x)+f(x)=1中,令x= 可得f(
可得f( )+f(
)+f( )=1即f(
)=1即f( )=
)=
同理可求f( )=
)=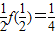 ,f(
,f( )=1-f(
)=1-f( )=
)=
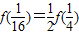 =
= ,f(
,f(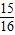 )=1-f(
)=1-f(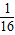 )=
)=
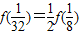 =
= ,f(
,f(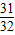 )=1-f(
)=1-f(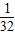 )=
)=
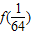 =
=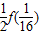 =
= ,f(
,f(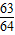 )=1-
)=1- =
=
∵当0≤x1≤x2≤1时,f(x1)≤f(x2),
∴ =
=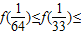 f(
f(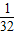 )=
)=
∴f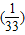 =
=
故选B
点评:本题主要考查了抽象函数及其应用,考查分析问题和解决问题的能力,属于中档题
 ),然后根据条件求出f
),然后根据条件求出f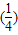 ,
,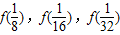 ,最后根据函数的单调性,以及两边夹的性质可求出所求.
,最后根据函数的单调性,以及两边夹的性质可求出所求.解答:解:∵f(1)=1,f(1-x)=1-f(x)
令x=
 得f(
得f( )+f(
)+f( )=1即f(
)=1即f( )=
)=
∵2f(x)=f(4x)
∴f(x)=
 f(4x)
f(4x)在f(x)=
 f(4x)中,令x=
f(4x)中,令x= 可得f(
可得f( )=
)=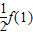 =
=
在f(1-x)+f(x)=1中,令x=
 可得f(
可得f( )+f(
)+f( )=1即f(
)=1即f( )=
)=
同理可求f(
 )=
)=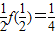 ,f(
,f( )=1-f(
)=1-f( )=
)=
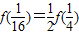 =
= ,f(
,f(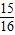 )=1-f(
)=1-f(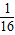 )=
)=
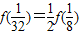 =
= ,f(
,f(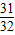 )=1-f(
)=1-f(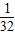 )=
)=
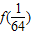 =
=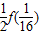 =
= ,f(
,f(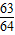 )=1-
)=1- =
=
∵当0≤x1≤x2≤1时,f(x1)≤f(x2),
∴
 =
=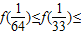 f(
f(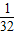 )=
)=
∴f
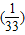 =
=
故选B
点评:本题主要考查了抽象函数及其应用,考查分析问题和解决问题的能力,属于中档题

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
已知定义在R上的函数f(x),对任意x∈R,都有f(x+6)=f(x)+f(3)成立,若函数y=f(x+1)的图象关于直线x=-1对称,则f(2013)=( )
| A、0 | B、2013 | C、3 | D、-2013 |