Question

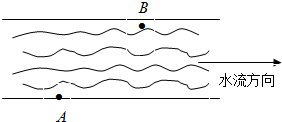
一条河的两岸平行，河宽400 m，一小船从A处出发航行到对岸，小船速度为v₁,且|v₁|=3 m/s，水流速度为v₂，|v₂|=2 m/s.

(1)当v₁、v₂夹角θ多大时，船才能到达对岸B处？此时位移的大小方向怎样？时间是多少？

(2)当v₁与v₂的夹角θ多大时，小船航行的时间最少？此时位移的大小方向怎样？时间为多少？

Answer 1

解：(1)如图，cosθ=,设小船实际航行的速度为v，

    则v=v₁+v₂且v⊥v₂,

∴cosθ==-,

θ=π-arccos,t==80(s).

答:当v₁、v₂夹角为π-arccos时,船能到对岸 B处，此时位移大小为400 m，方向由A指向正对岸，时间为80s.

(2)小船在AB上的分速度为|v₁|=3sinθ,||=400,∴t=.

    当θ=90°时，t取最小值(如下图).

    此时t_min=,位移的大小为

|v|=×.

    设位移与水流方向的夹角为α，则α=arctan.

答:当v₁与v₂垂直时，小船航行的时间最少，为s，此时位移的大小为，方向为与水流方向成arctan的角.