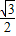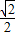Question

求证：正四面体的二面角与正八面体的二面角互为补角.

Answer 1

证明:设正四面体S—ABC和正八面体AC的棱长都为a，正四面体的二面角为α，正八面体的二面角为2β.

在正四面体S—ABC中(图甲)，作SG⊥底面ABC于G，连结AG并延长交BC于D，连结SD.

∴G为正△ABC的中心.

∴AD⊥BD.

∴SD⊥BC(三垂线定理).

∴∠SDG为二面角的平面角，即∠SDG=α.

又AD=SD=,

∴SG=a.

∴tanα=(0°＜α＜90°).

              

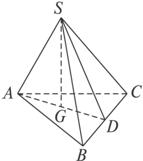
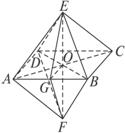
                   甲                                           乙

在正八面体AC中(图乙)，连结EF交截面ABCD于O，取AB的中点G，连结EG、FG、OG，则EG⊥AB，FG⊥AB，

∴∠EGF为二面角的平面角，由对称性知，∠EGO=∠OGF=β.

又EG=a,GO=a,∴EO=a.

∴tan∠EGO=tanβ=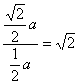 (0°＜β＜90°).

∴tan2β=.

∴tan(α+2β)=.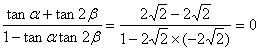

∵0°＜α+2β＜270°,

∴α+2β=180°.

∴正四面体和正八面体的二面角互补.