题目内容
已知λ，x∈R，命题p：x2-3x+2＞0，命题q：存在实数λ使得
，则
（1）写出p的否定，判断真假并说明理由；
（2）写出q的否命题，判断真假并说明理由．
解：（1）命题p：x2-3x+2＞0，的否定：?x∈R，x2-3x+2≤0，
∵x=1时，x2-3x+2=0，∴此命题为真；
（2）命题q：存在实数λ使得，则否命题是：
?λ∈R，都有
，则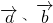
不平行，其是假命题．
∵
，
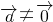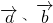，?λ∈R，都有使得，则平行．
分析：（1）已知命题命题p：x2-3x+2＞0，是全称命题，根据命题否定的规则进行求解；
（2）将命题的条件否定结论也否定，可得否命题．再用举反例的方法，可得它也是一个假命题．
点评：命题的否定即命题的对立面．“全称量词”与“存在量词”正好构成了意义相反的表述．如“任意”与“存的”，“对所有的…都成立”与“至少有一个…不成立”；“都是”与“不都是”等．注意命题的否定与否命题的不同之处．
∵x=1时，x2-3x+2=0，∴此命题为真；
（2）命题q：存在实数λ使得
，则否命题是：?λ∈R，都有
，则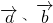不平行，其是假命题．∵
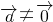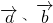，，?λ∈R，都有使得，则平行．分析：（1）已知命题命题p：x2-3x+2＞0，是全称命题，根据命题否定的规则进行求解；
（2）将命题的条件否定结论也否定，可得否命题．再用举反例的方法，可得它也是一个假命题．
点评：命题的否定即命题的对立面．“全称量词”与“存在量词”正好构成了意义相反的表述．如“任意”与“存的”，“对所有的…都成立”与“至少有一个…不成立”；“都是”与“不都是”等．注意命题的否定与否命题的不同之处．
练习册系列答案
相关题目