题目内容
 (2012•黄浦区二模)已知三棱锥P-ABC,PA⊥平面ABC,AB⊥AC,AB=AC=4,AP=5.
(2012•黄浦区二模)已知三棱锥P-ABC,PA⊥平面ABC,AB⊥AC,AB=AC=4,AP=5.(1)求二面角P-BC-A的大小(结果用反三角函数值表示).
(2)把△PAB(及其内部)绕PA所在直线旋转一周形成一几何体,求该几何体的体积V.
分析:(1)取BC中点D,连接AD、PD,可得∠PDA为二面角P-BC-A的平面角,在直角△PAD中,利用正切函数可求二面角P-BC-A的大小;
(2)由题设,所得几何体为圆锥,其底面半径为4,高为5,故可求圆锥的体积.
(2)由题设,所得几何体为圆锥,其底面半径为4,高为5,故可求圆锥的体积.
解答:解:(1)取BC中点D,连接AD、PD;
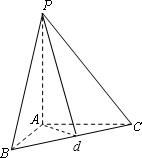
在等腰三角形PBC、ABC中,PD⊥BC,AD⊥BC,故∠PDA为二面角P-BC-A的平面角. (2分)
在等腰直角△ABC中,由AB=AC=4及AB⊥AC,得AD=2
.
由PA⊥平面ABC,得PA⊥AD.
在直角△PAD中,tan∠PDA=
=
. (6分)
故二面角P-BC-A的大小为arctan
. (8分)
(2)由题设,所得几何体为圆锥,其底面半径为4,高为5.
∴该圆锥的体积V=
×5×π×42=
. (12分)

在等腰三角形PBC、ABC中,PD⊥BC,AD⊥BC,故∠PDA为二面角P-BC-A的平面角. (2分)
在等腰直角△ABC中,由AB=AC=4及AB⊥AC,得AD=2
| 2 |
由PA⊥平面ABC,得PA⊥AD.
在直角△PAD中,tan∠PDA=
| PA |
| AD |
5
| ||
| 4 |
故二面角P-BC-A的大小为arctan
5
| ||
| 4 |
(2)由题设,所得几何体为圆锥,其底面半径为4,高为5.
∴该圆锥的体积V=
| 1 |
| 3 |
| 80π |
| 3 |
点评:本题考查面面角,考查几何体体积的计算,正确确定面面角是解题的关键.

练习册系列答案
相关题目
 (2012•黄浦区二模)如图,已知圆柱的轴截面ABB1A1是正方形,C是圆柱下底面弧AB的中点,C1是圆柱上底面弧A1B1的中点,那么异面直线AC1与BC所成角的正切值为
(2012•黄浦区二模)如图,已知圆柱的轴截面ABB1A1是正方形,C是圆柱下底面弧AB的中点,C1是圆柱上底面弧A1B1的中点,那么异面直线AC1与BC所成角的正切值为