题目内容
已知平行六面体ABCD-A′B′C′D′中,AB=4,AD=3,AA′=5,∠BAD=90°,∠BAA′=∠DAA′=60°,(1)求AC′的长;(如图所示)
(2)求
 与
与 的夹角的余弦值.
的夹角的余弦值.
【答案】分析:(1)可得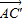 =
=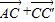 =
=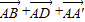 ,由数量积的运算可得
,由数量积的运算可得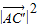 ,开方可得;(2)由(1)可知
,开方可得;(2)由(1)可知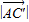 ,又可求
,又可求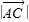 和
和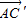
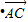 ,代入夹角公式可得.
,代入夹角公式可得.
解答:解:(1)可得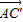 =
=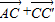 =
=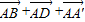 ,
,
故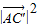 =
=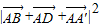 =
=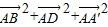
+2(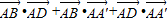 )
)
=42+32+52+2(4×3×0+4×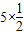
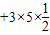 )=85
)=85
故AC′的长等于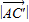 =
=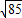
(2)由(1)可知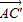 =
=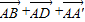 ,
,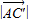 =
=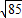
故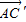
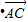 =(
=(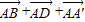 )•(
)•(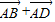 )
)
=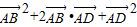
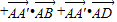
=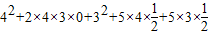 =
=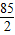
又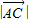 =
=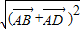 =
=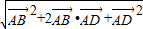 =
=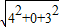 =5
=5
故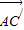 与
与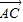 的夹角的余弦值=
的夹角的余弦值=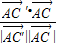 =
=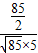 =
=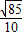
点评:本题考查空间向量的模长和夹角的余弦值的运算,化向量为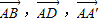 是解决问题的关键,属中档题.
是解决问题的关键,属中档题.
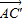 =
=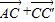 =
=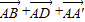 ,由数量积的运算可得
,由数量积的运算可得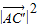 ,开方可得;(2)由(1)可知
,开方可得;(2)由(1)可知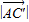 ,又可求
,又可求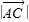 和
和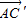
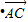 ,代入夹角公式可得.
,代入夹角公式可得.解答:解:(1)可得
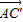 =
=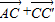 =
=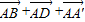 ,
,故
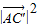 =
=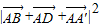 =
=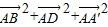
+2(
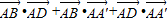 )
)=42+32+52+2(4×3×0+4×
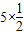
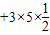 )=85
)=85故AC′的长等于
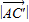 =
=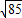
(2)由(1)可知
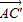 =
=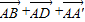 ,
,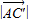 =
=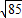
故
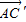
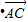 =(
=(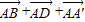 )•(
)•(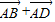 )
)=
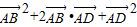
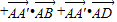
=
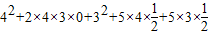 =
=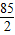
又
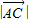 =
=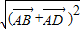 =
=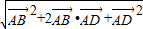 =
=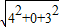 =5
=5故
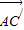 与
与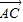 的夹角的余弦值=
的夹角的余弦值=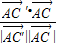 =
=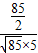 =
=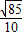
点评:本题考查空间向量的模长和夹角的余弦值的运算,化向量为
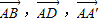 是解决问题的关键,属中档题.
是解决问题的关键,属中档题. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O. 如图,已知平行六面体ABCD-A1B1C1D1.
如图,已知平行六面体ABCD-A1B1C1D1.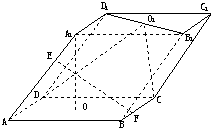 如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O. 如图,已知平行六面体ABCD-A1B1C1D1.
如图,已知平行六面体ABCD-A1B1C1D1.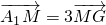 ,设
,设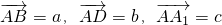 ,用向量a、b、c表示向量
,用向量a、b、c表示向量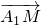 ;
;