Question

【题目】在直角坐标系中，已知圆的圆心坐标为，半径为，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，直线l的参数方程为：（为参数）．

（1）求圆和直线l的极坐标方程；

（2）点的极坐标为，直线l与圆相交于A，B，求的值．

Answer 1

【答案】（1）圆的极坐标方程为， 的极坐标方程为；（2）．

【解析】

（1）代入圆C得圆C的极坐标方程；直线l的参数方程转化成普通方程，进而求得直线l的极坐标方程；（2）将直线l的参数方程代入圆的方程，求得关于t的一元二次方程，令A，B对应参数分别为t1，t2，根据韦达定理、直线与圆的位置关系，即可求得|PA|+|PB|的值．

（1）圆的直角坐标方程为：，

把代入圆得：

化简得圆的极坐标方程为：

由 （为参数），得，

的极坐标方程为：.

（2）由点的极坐标为得点的直角坐标为，

∴直线的参数方程可写成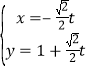：（为参数）．

代入圆得：化简得：，

∴，，

∴．