题目内容
 如图所示,大风车的半径为2m,每12s旋转一周,它的最低点O离地面0.5m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为h(m).
如图所示,大风车的半径为2m,每12s旋转一周,它的最低点O离地面0.5m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为h(m).(1)求函数h=f(t)的关系式.
(2)画出函数h=f(t的图象.
【答案】分析:(1)以圆心O为原点,以水平方向为x轴方向,以竖直方向为Y轴方向建立平面直角坐标系,则根据大风车的半径为2m,圆上最低点与地面距离为0.5m,12s秒转动一圈,我们易得到到h与t间的函数关系式;
(2)结合(1)中三角函数的解析式,再根据解析式画出函数的图象.
解答: 解:(1)以圆心O为原点,建立如图所示的平面直角坐标系,
解:(1)以圆心O为原点,建立如图所示的平面直角坐标系,
则以Ox为始边,OB为终边的角为 θ-
θ- ,
,
故点B的坐标为
(2cos ,2sin
,2sin  ),
),
∴h=2.5+2sin =-2cos(
=-2cos( )+2.5.
)+2.5.
(2)图象如图:

点评:本题考查的知识点是在实际问题中建立三角函数模型,在建立函数模型的过程中,以圆心O为原点,以水平方向为x轴方向,以竖直方向为Y轴方向建立平面直角坐标系,将现实问题转化为数学问题,是解答的关键.
(2)结合(1)中三角函数的解析式,再根据解析式画出函数的图象.
解答:
 解:(1)以圆心O为原点,建立如图所示的平面直角坐标系,
解:(1)以圆心O为原点,建立如图所示的平面直角坐标系,则以Ox为始边,OB为终边的角为
 θ-
θ- ,
,故点B的坐标为
(2cos
 ,2sin
,2sin  ),
),∴h=2.5+2sin
 =-2cos(
=-2cos( )+2.5.
)+2.5.(2)图象如图:

点评:本题考查的知识点是在实际问题中建立三角函数模型,在建立函数模型的过程中,以圆心O为原点,以水平方向为x轴方向,以竖直方向为Y轴方向建立平面直角坐标系,将现实问题转化为数学问题,是解答的关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
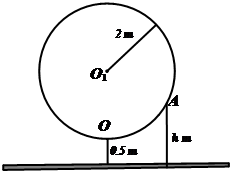 如图所示,大风车的半径为2m,每12s旋转一周,它的最低点O离地面0.5m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为h(m).
如图所示,大风车的半径为2m,每12s旋转一周,它的最低点O离地面0.5m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为h(m). 如图所示,大风车的半径为2m,每12s旋转一周,它的最低点O离地面0.5m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为h(m).
如图所示,大风车的半径为2m,每12s旋转一周,它的最低点O离地面0.5m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为h(m). 如图所示,大风车的半径为2m,每12s旋转一周,它的最低点O离地面0.5m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为h(m).
如图所示,大风车的半径为2m,每12s旋转一周,它的最低点O离地面0.5m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为h(m). 如图所示,大风车的半径为2m,每12s旋转一周,它的最低点O离地面0.5m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为h(m).
如图所示,大风车的半径为2m,每12s旋转一周,它的最低点O离地面0.5m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为h(m).