题目内容
若方程y=x+m与y=
有且只有一个解,求实数m的取值范围.
| 4-x2 |
分析:由题意可得直线y=x+m与半圆y=
只有一个交点,数形结合可得实数m的取值范围.
| 4-x2 |
解答:解:∵曲线y=
表示半圆 x2+y2=4( y≥0),由题意可得直线y=x+m与半圆 y=
只有一个交点,
∴利用数形结合可得-2≤m<2,或 m=2
.
故实数m的取值范围是{m|-2≤m<2,或 m=2
}.

| 4-x2 |
| 4-x2 |
∴利用数形结合可得-2≤m<2,或 m=2
| 2 |
故实数m的取值范围是{m|-2≤m<2,或 m=2
| 2 |

点评:本题主要考查函数的零点的定义,函数的零点与方程的根的关系,体现了转化、数形结合的数学思想,属于基础题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
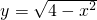 有且只有一个解,求实数m的取值范围.
有且只有一个解,求实数m的取值范围.