题目内容
平面直角坐标系中，已知A（1-
，1）、P（-
，0），O为原点，等腰△AOB底边AB与y轴垂直，过点P的直线与△AOB围成的区域有公共点，则直线与y轴的交点保持在该区域内部的概率为：
．
| 3 |
| 3 |
| ||
| 3 |
| ||
| 3 |
分析：根据题意作出图形，如图所示．本题利用几何概型求概率．若过点P的直线与△AOB围成的区域有公共点，则直线与y轴的交点保持在线段OC上，而直线与y轴的交点保持在该区域内部时，直线与y轴的交点保持在线段OD上，从而得出直线与y轴的交点保持在该区域内部的概率为：P=
即可得出答案．
| OD |
| OC |
解答：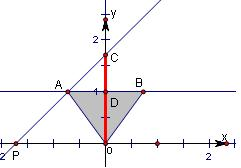
解：如图，等腰△AOB底边AB与y轴垂直，
若过点P的直线与△AOB围成的区域有公共点，则直线与y轴的交点保持在线段OC上，由已知A（1-
，1）、P（-
，0），得C（0，
）．
而直线与y轴的交点保持在该区域内部时，直线与y轴的交点保持在线段OD上，
根据几何概型的概率公式得，直线与y轴的交点保持在该区域内部的概率为：P=
=
=
．
故答案为：
．
解：如图，等腰△AOB底边AB与y轴垂直，若过点P的直线与△AOB围成的区域有公共点，则直线与y轴的交点保持在线段OC上，由已知A（1-
| 3 |
| 3 |
| 3 |
而直线与y轴的交点保持在该区域内部时，直线与y轴的交点保持在线段OD上，
根据几何概型的概率公式得，直线与y轴的交点保持在该区域内部的概率为：P=
| OD |
| OC |
| 1 | ||
|
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题考查几何概型概率的求法，是基础题．解题时要认真审题，注意直线与y轴的交点保持在该区域内部所形成的线段区域的长度的求法．
练习册系列答案
相关题目
