Question

 [例] 设,函数.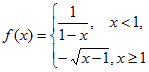

试讨论函数的单调性.

Answer 1

①当k=0时，F(x)在区间上单调递增，F(x)在区间上单调递减；

②当k<0时，F(x)在区间上单调递增，在区间上单调递减,在区间

上单调递增；③当时，F(x)在区间上单调递减,在区间

上单调递增,在区间上单调递减.

解析:

分段函数要分段处理，由于每一段都是基本初等函数的复合函数，所以应该用导数来研究。

因为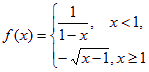,所以.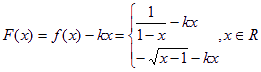

 (1)当x<1时，1-x>0，

 ①当时，在上恒成立，故F(x)在区间上单调递增；

 ②当时，令，解得，

 且当时，；当时，

 故F(x)在区间上单调递减,在区间上单调递增；

(2)当x>1时， x-1>0，

 ①当时，在上恒成立，故F(x)在区间上单调递减；

 ②当时，令，解得，

且当时，；当时，

故F(x)在区间上单调递减,在区间上单调递增；

综上得，①当k=0时，F(x)在区间上单调递增，F(x)在区间上单调递减；

②当k<0时，F(x)在区间上单调递增，在区间上单调递减,在区间

上单调递增；③当时，F(x)在区间上单调递减,在区间

上单调递增,在区间上单调递减.