题目内容
已知抛物线C以原点为顶点,焦点F在x轴上,其准线交x轴于点N,点M(1,m)在抛物线C上,且|MF|=2.(1)求抛物线C的方程;
(2)记抛物线的准线交x轴于点N,过点N直线l交抛物线于A、B两点,若△ABF的面积为
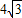 ,求直线l的方程.
,求直线l的方程.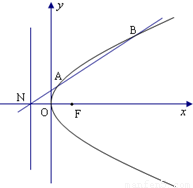
【答案】分析:(1)由题意,设抛物线方程为y2=2px(p>0),根据点M(1,m)在抛物线C上,且|MF|=2,可求得p=2,从而可确定抛物线方程;
(2)点N(-1,0),设直线l方程为x=ky-1代入抛物线方程,利用△ABF的面积为 ,可求k=±2,故可求直线l的方程.
,可求k=±2,故可求直线l的方程.
解答:解:(1)由题意,设抛物线方程为y2=2px(p>0)
∵点M(1,m)在抛物线C上,且|MF|=2
∴
∴p=2
∴抛物线方程为 y2=4x.
(2)点N(-1,0),设直线l方程为x=ky-1
代入抛物线方程y2=4x,得y2-4ky+4=0
设A(x1,y1),B(x2,y2),则
∵△ABF的面积为
∴
∴16k2-16=48
∴k=±2
∴直线l的方程x=±2y-1.
经检验,符合题意.
点评:本题以抛物线为载体,考查抛物线的定义,考查直线与抛物线的位置关系,考查面积公式.
(2)点N(-1,0),设直线l方程为x=ky-1代入抛物线方程,利用△ABF的面积为
 ,可求k=±2,故可求直线l的方程.
,可求k=±2,故可求直线l的方程.解答:解:(1)由题意,设抛物线方程为y2=2px(p>0)
∵点M(1,m)在抛物线C上,且|MF|=2
∴

∴p=2
∴抛物线方程为 y2=4x.
(2)点N(-1,0),设直线l方程为x=ky-1
代入抛物线方程y2=4x,得y2-4ky+4=0
设A(x1,y1),B(x2,y2),则
∵△ABF的面积为

∴

∴16k2-16=48
∴k=±2
∴直线l的方程x=±2y-1.
经检验,符合题意.
点评:本题以抛物线为载体,考查抛物线的定义,考查直线与抛物线的位置关系,考查面积公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知抛物线C以原点为顶点,焦点F在x轴上,其准线交x轴于点N,点M(1,m)在抛物线C上,且|MF|=2.
已知抛物线C以原点为顶点,焦点F在x轴上,其准线交x轴于点N,点M(1,m)在抛物线C上,且|MF|=2.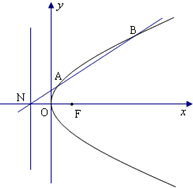 已知抛物线C以原点为顶点,焦点F在x轴上,其准线交x轴于点N,点M(1,m)在抛物线C上,且|MF|=2.
已知抛物线C以原点为顶点,焦点F在x轴上,其准线交x轴于点N,点M(1,m)在抛物线C上,且|MF|=2. ,求直线l的方程.
,求直线l的方程. 为定值;
为定值;