Question

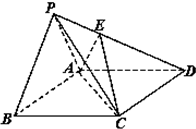如图，四棱锥P-ABCD中，△PAB为边长为2的正三角形，底面ABCD为菱形，且平面PAB⊥平面ABCD，PC⊥AB，E为PD点上一点，满足

PE

=

1

2

ED

（Ⅰ）证明：平面ACE⊥平面ABCD；
（Ⅱ）求直线PD与平面ACE所成角正弦值的大小．

Answer 1

分析：（I）取AB的中点O，连接PO，OC，根据等腰三角形三线合一及面面垂直的性质定理和线面垂直的性质，可得PO⊥平面ABCD及AB⊥OC，以O为坐标原点，建立空间坐标系，分别求出平面ACE和平面ABCD的法向量，代入向量夹角公式，可得结论
（Ⅱ）求出直线PD的方向，结合（I）中平面ACE的法向量，代入向量夹角公式，可得直线PD与平面ACE所成角正弦值的大小．

解答：证明：（I）取AB的中点O，连接PO，OC
∵△PAB为边长为2的正三角形，
∴PO⊥AB
又∵平面PAB⊥平面ABCD，平面PAB∩平面ABCD=AB，PO?平面PAB
∴PO⊥平面ABCD，

又∵PC⊥AB，PO∩PC=P，PO，PC?平面POC
∴AB⊥平面POC
又∵OC?平面POC
∴AB⊥OC
以O为坐标原点，建立如图所示的空间坐标系，
则A（-1，0，0），C（0，

3

，0），P（0，0，

3

），D（-2，

3

，0）
∵

PE

=

1

2

ED

则E（-

2

3

，

3

3

，

2 3

3

）
则

AC

=（1，

3

，0），

AE

=（

1

3

，

3

3

，

2 3

3

）
设平面ACE的法向量为

n

=（x，y，z）
则由

n ⊥ AC n ⊥ AE

可得

n • AC =0 n • AE =0

即

x+ 3 y=0 1 3 x+ 3 3 y+ 2 3 3 z=0

令x=1，则

n

=（1，-

3

3

，0）
取平面ABCD的一个法向量

OP

=（0，0，

3

），
则

n

•

OP

=0，即

n

⊥

OP

故平面ACE⊥平面ABCD；
（Ⅱ）设直线PD与平面ACE所成角的大小为θ．
∵直线PD的方向向量

PD

=（-2，

3

，-

3

），平面ACE的法向量

n

=（1，-

3

3

，0）
∴sinθ=

| PD • n |

| PD |•| n |

=

3 30

20

故直线PD与平面ACE所成角正弦值为

3 30

20

点评：本题考查的知识点是平面与平面垂直的判定，直线与平面所成的解，其中建立空间坐标系，将空间面面垂直问题和线面夹角问题，转化为向量垂直和向量夹角问题是解答的关键．