题目内容
14.解不等式组$\left\{\begin{array}{l}{{x}^{2}-x-6≥0}\\{\frac{x+1}{x-2}>2}\end{array}\right.$.分析 由x2-x-6≥0,化为(x-3)(x+2)≥0,解得x范围.由$\frac{x+1}{x-2}$>2,化为$\frac{x-5}{x-2}$<0,化为(x-2)(x-5)<0,解得x范围,求其交集即可.
解答 解:由x2-x-6≥0,化为(x-3)(x+2)≥0,解得x≥3或x≤-2.
由$\frac{x+1}{x-2}$>2,化为$\frac{x-5}{x-2}$<0,化为(x-2)(x-5)<0,解得2<x<5.
联立$\left\{\begin{array}{l}{x≥3或x≤-2}\\{2<x<5}\end{array}\right.$,
解得3≤x<5.
∴不等式组的解集为[3,5).
点评 本题查克拉一元二次不等式的解法、分式不等式的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.集合A={x|x2-2x-3<0},B={x|x2<p},若B?A,则实数p的取值范围是( )
| A. | (0,1] | B. | (-∞,1] | C. | (-1,3] | D. | (-∞,1) |
6.已知正项数列{an}满足a1=1,(n+2)an+12-(n+1)a${\;}_{n}^{2}$+anan+1=0,则它的通项公式为( )
| A. | an=$\frac{1}{n+1}$ | B. | an=$\frac{2}{n+1}$ | C. | an=$\frac{n+1}{2}$ | D. | an=n |
4.2008年5月12日,四川汶川地区发生里氏8.0级特大地震.在随后的几天中,地震专家对汶川地区发生的余震进行了监测.记录的部分数据如下表:
(注:地震强度是指地震时释放的能量)
(1)画出震级(y)随地震强度(x)的变化散点图;
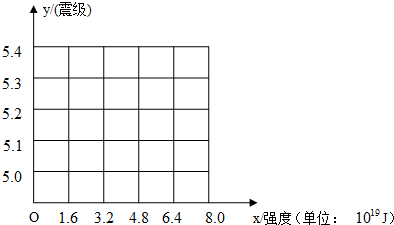
(2)根据散点图,从函数y=kx+b,y=algx+b,y=a•10x+b中选取一个函数描述震级y随地震强度x的变化关系;
(3)四川汶川地区发生里氏8.0级特大地震时释放的能量约是多少?(取lg2=0.3)
| 强度(J) | 1.6×1019 | 3.2×1019 | 4.5×1019 | 6.4×1019 |
| 震级(里氏) | 5.0 | 5.2 | 5.3 | 5.4 |
(1)画出震级(y)随地震强度(x)的变化散点图;

(2)根据散点图,从函数y=kx+b,y=algx+b,y=a•10x+b中选取一个函数描述震级y随地震强度x的变化关系;
(3)四川汶川地区发生里氏8.0级特大地震时释放的能量约是多少?(取lg2=0.3)