题目内容
(1)设函数f(x)=xlnx+(1﹣x)ln(1﹣x)(0<x<1),求f(x)的最小值;
(2)设正数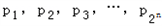 满足
满足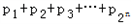 =1,求证:
=1,求证:
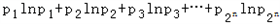 ≥﹣n.
≥﹣n.
(2)设正数
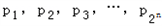 满足
满足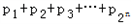 =1,求证:
=1,求证: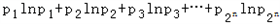 ≥﹣n.
≥﹣n.(1)解:对函数f(x)求导数:f'(x)=(xlnx)'+[(1﹣x)ln(1﹣x)]'=lnx﹣ln(1﹣x).
于是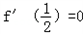 .
.
当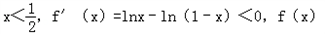 在区间
在区间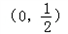 是减函数,
是减函数,
当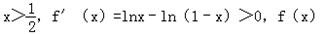 在区间
在区间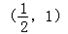 是增函数.
是增函数.
所以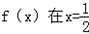 时取得最小值,
时取得最小值,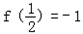 ,
,
(2)用数学归纳法证明.
(i)当n=1时,由(1)知命题成立.
(ii)假定当n=k时命题成立,即若正数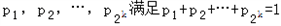 ,则
,则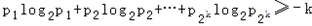 .
.
当n=k+1时,若正数 ,
,
令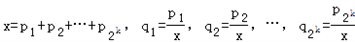 .
.
则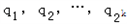 为正数,且
为正数,且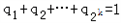 .
.
由归纳假定知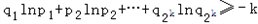 .
.
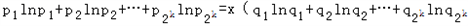 +lnx)≥x(﹣k)+xlnx,①同理,由
+lnx)≥x(﹣k)+xlnx,①同理,由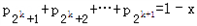 可得
可得
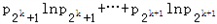 ≥(1﹣x)(﹣k)+(1﹣x)n(1﹣x).
≥(1﹣x)(﹣k)+(1﹣x)n(1﹣x).
②综合①、②两式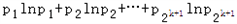
≥[x+(1﹣x)](﹣k)+xlnx+(1﹣x)ln(1﹣x)≥﹣(k+1).
即当n=k+1时命题也成立.根据(i)、(ii)可知对一切正整数n命题成立.
于是
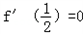 .
.当
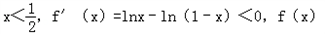 在区间
在区间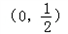 是减函数,
是减函数,当
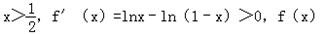 在区间
在区间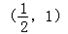 是增函数.
是增函数.所以
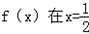 时取得最小值,
时取得最小值,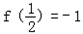 ,
,(2)用数学归纳法证明.
(i)当n=1时,由(1)知命题成立.
(ii)假定当n=k时命题成立,即若正数
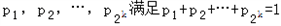 ,则
,则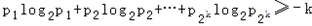 .
.当n=k+1时,若正数
 ,
,令
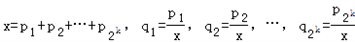 .
.则
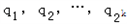 为正数,且
为正数,且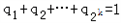 .
.由归纳假定知
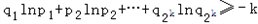 .
.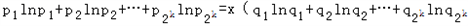 +lnx)≥x(﹣k)+xlnx,①同理,由
+lnx)≥x(﹣k)+xlnx,①同理,由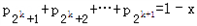 可得
可得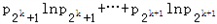 ≥(1﹣x)(﹣k)+(1﹣x)n(1﹣x).
≥(1﹣x)(﹣k)+(1﹣x)n(1﹣x).②综合①、②两式
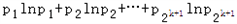
≥[x+(1﹣x)](﹣k)+xlnx+(1﹣x)ln(1﹣x)≥﹣(k+1).
即当n=k+1时命题也成立.根据(i)、(ii)可知对一切正整数n命题成立.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目