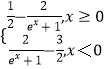题目内容
【题目】已知集合A={x|﹣4<x<1},B={x|( ![]() )x≥2}.
)x≥2}.
(1)求A∩B,A∪B;
(2)设函数f(x)= ![]() 的定义域为C,求(RA)∩C.
的定义域为C,求(RA)∩C.
【答案】
(1)解:由( ![]() )x≥2得(
)x≥2得( ![]() )x≥=(
)x≥=( ![]() )﹣1,
)﹣1,
则x≤﹣1,即B={x|x≤﹣1},
∵A={x|﹣4<x<1},
∴A∩B={x|﹣4<x≤﹣1},A∪B={x|x<1}
(2)解:由题意得, ![]() ,
,
即 ![]() ,解得x≥2,
,解得x≥2,
∴函数f(x)的定义域C={x|x≥2},
由A={x|﹣4<x<1}得,RA={x|x≤﹣4或x≥1},
∴(RA)∩C={x|x≥2}
【解析】(1)由指数的运算、指数函数的性质求出B,由交、并集的运算分别求出A∩B,A∪B;(2)由对数函数的性质求出定义域C,由补、交集的运算分别求出RA,RA)∩C.
【考点精析】解答此题的关键在于理解交、并、补集的混合运算的相关知识,掌握求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法.

【题目】某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,
(单位:元),继续购买该险种的投保人称为续保人,
续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 |
|
|
|
|
|
|
随机调查了该险种的400名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 |
|
频数 | 120 | 100 | 60 | 60 | 40 | 20 |
(Ⅰ)记A为事件:“一续保人本年度的保费不高于基本保费”.求![]() 的估计值;
的估计值;
(Ⅱ)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的190%”.
求![]() 的估计值;
的估计值;
(III)求续保人本年度的平均保费估计值.
【题目】“累积净化量![]() ”是空气净化器质量的一个重要衡量指标,它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示,根据
”是空气净化器质量的一个重要衡量指标,它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示,根据![]() 《空气净化器》国家标准,对空气净化器的累计净化量
《空气净化器》国家标准,对空气净化器的累计净化量![]() 有如下等级划分:
有如下等级划分:
累积净化量(克) |
|
|
| 12以上 |
等级 |
|
|
|
|
为了了解一批空气净化器(共5000台)的质量,随机抽取![]() 台机器作为样本进行估计,已知这
台机器作为样本进行估计,已知这![]() 台机器的累积净化量都分布在区间
台机器的累积净化量都分布在区间![]() 中,按照
中,按照![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 均匀分组,其中累积净化量在
均匀分组,其中累积净化量在![]() 的所有数据有:4.5,4.6,5.2,5.3,5.7和5.9,并绘制了频率分布直方图,如图所示:
的所有数据有:4.5,4.6,5.2,5.3,5.7和5.9,并绘制了频率分布直方图,如图所示:
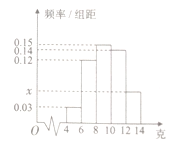
(1)求![]() 的值及频率分布直方图中
的值及频率分布直方图中![]() 的值;
的值;
(2)以样本估计总体,试估计这批空气净化器(共5000台)中等级为![]() 的空气净化器有多少台?
的空气净化器有多少台?
(3)从累积净化量在![]() 的样本中随机抽取2台,求恰好有1台等级为
的样本中随机抽取2台,求恰好有1台等级为![]() 的概率.
的概率.