题目内容
如图,正方体 中,点
中,点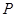 为线段
为线段 上一动点,点
上一动点,点 为底面
为底面 内(含边界)一动点,
内(含边界)一动点, 为
为 的中点,点
的中点,点 构成的点集是一个空间几何体,则该几何体为( )
构成的点集是一个空间几何体,则该几何体为( )
| A.棱柱 | B.棱锥 |
| C.棱台 | D.球 |
A
解析试题分析:先固定 点位置,
点位置, 点在底面
点在底面 的边界上运动时,连接
的边界上运动时,连接 ,则
,则 的中点
的中点 就在
就在 的中位线上运动,如图中
的中位线上运动,如图中 ,当
,当 在底面
在底面 内部运动时,
内部运动时, 就在
就在 内部运动;且
内部运动;且 ∥
∥ ,
, 与
与 相似,
相似, 的面积是
的面积是 的面积一半;当
的面积一半;当 点运动到
点运动到 时,同理可知
时,同理可知 点轨迹是
点轨迹是 内部及边界,且
内部及边界,且 ∥
∥ ,
, 与
与 相似,
相似, 的面积是
的面积是 的面积一半,所以
的面积一半,所以 ∥
∥ ,
, ≌
≌ ,则
,则 构成的点集是一个空间几何体是棱柱,故选A.
构成的点集是一个空间几何体是棱柱,故选A.
考点:对空间图形的认识.

练习册系列答案
相关题目
若一个空间几何体的三视图如图所示,则这个几何体的表面积为
A. | B.4 |
C. | D.8 |
一个几何体的三视图如图所示,则该几何体的体积为( )
A. | B. | C. | D. |
如果两个球的体积之比为8:27,那么两个球的表面积之比为( )
| A.8:27 | B.2:3 | C.4:9 | D.2:9 |
(2012•广东)某几何体的三视图如图所示,它的体积为( )
| A.12π | B.45π | C.57π | D.81π |
某几何体的三视图如下图所示,它的体积为( )
A. |
B. |
C. |
D. |
正方体内切球和外接球半径的比为( )
A. |
B. |
C. |
| D.1:2 |




