题目内容
已知f(x)是定义在[-1,1]上的奇函数,且f(1)=1,若a、b∈[-1,1],a+b≠0,有(1)判断函数f(x)在[-1,1]上的单调性,并证明你的结论;
(2)解不等式f(x+![]() )<f(
)<f(![]() ).
).
解:(1)∵f(x)是[-1,1]上的奇函数,
∴f(0)=0.
又知f(1)=1,
∴f(-1)=-f(1)=-1,从而可判断函数f(x)在[-1,1]上是增函数.
证明如下:由题设,若a、b∈[-1,1],a+b≠0,有![]() >0.
>0.
令x1=-a,x2=b,则∵a、b∈[-1,1],∴x1、x2∈[-1,1].
由![]() >0得
>0得![]() >0.
>0.
∴![]() >0.
>0.
∴当x1<x2时,有f(x2)-f(x1)>0.
当x1>x2时,有f(x2)-f(x1)<0,即f(x)为增函数.
(2)由f(x+![]() )<f(
)<f(![]() )及题设及(1)知
)及题设及(1)知
解之,得
∴-![]() ≤x<-1,
≤x<-1,
即原不等式的解集为{x|-![]() ≤x<-1}.
≤x<-1}.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
 ) =
f(x)-f(y)
) =
f(x)-f(y) 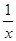 ) <2
) <2  ∪
∪ 上的奇函数,当
上的奇函数,当 时,f (x)的图象如图所示,那么f (x)的值域是
时,f (x)的图象如图所示,那么f (x)的值域是
