题目内容
 甲船在A处测得乙船在北偏东60°方向的B处,两船相距5海里,且乙船正沿着南偏东45°方向以每小时14海里的速度航行.经过半小时,甲船在C处追上乙船,问甲船的航行方向是南偏东多少度(精确到1度)?航行的速度是每小时多少海里(精确到1海里)?
甲船在A处测得乙船在北偏东60°方向的B处,两船相距5海里,且乙船正沿着南偏东45°方向以每小时14海里的速度航行.经过半小时,甲船在C处追上乙船,问甲船的航行方向是南偏东多少度(精确到1度)?航行的速度是每小时多少海里(精确到1海里)?
分析:在△ABC中,利用余弦定理可以求得AC距离,进而可求甲船的速度;利用正弦定理可求∠BAC,从而可求甲船的航行方向.
解答:解: 由已知,∠ABC=105°,AB=5,BC=7,…(1分)
由已知,∠ABC=105°,AB=5,BC=7,…(1分)
所以AC2=AB2+BC2-2•AB•BC•cos∠ABC=25+49-70•
≈92.2,…(4分)
所以AC≈9.6(海里),…(5分)
所以甲船的速度为
=19.2,…(6分)
由正弦定理,
=
,
=
,…(8分)sin∠BAC=
•
≈0.70432,…(10分)
∠BAC≈450.…(11分)
所以甲船的航行方向是南偏东750,航行速度是每小时19海里.…(12分)
 由已知,∠ABC=105°,AB=5,BC=7,…(1分)
由已知,∠ABC=105°,AB=5,BC=7,…(1分)所以AC2=AB2+BC2-2•AB•BC•cos∠ABC=25+49-70•
| ||||
| 4 |
所以AC≈9.6(海里),…(5分)
所以甲船的速度为
| 9.6 |
| 0.5 |
由正弦定理,
| AC |
| sin∠ABC |
| BC |
| sin∠BAC |
| 9.6 | ||||||
|
| 7 |
| sin∠BAC |
| 7 |
| 9.6 |
| ||||
| 4 |
∠BAC≈450.…(11分)
所以甲船的航行方向是南偏东750,航行速度是每小时19海里.…(12分)
点评:本题的考点是已知三角函数模型的应用问题,主要考查解三角形的实际应用.解决这一类型题目的关键是把文字语言转化为数学符号,用数学公式,定理,公理等知识来解.

练习册系列答案
相关题目
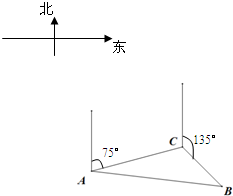 如图,甲船在A处测得:“乙船位于北偏东75°,距离为10海里的C处,并正沿着北偏东135°的方向,以每小时12海里的速度驶去.”经过半小时,甲船在B处追上了乙船.求:
如图,甲船在A处测得:“乙船位于北偏东75°,距离为10海里的C处,并正沿着北偏东135°的方向,以每小时12海里的速度驶去.”经过半小时,甲船在B处追上了乙船.求:
