题目内容
已知函数![]()
(1)当![]() 恒成立,求实数m的最大值;
恒成立,求实数m的最大值;
(2)在曲线![]() 上存在两点关于直线
上存在两点关于直线![]() 对称,求t的取值范围;
对称,求t的取值范围;
(3)在直线![]() 的两条切线l1、l2,求证:l1⊥l2
的两条切线l1、l2,求证:l1⊥l2
解析:(1)直线y=x与曲线![]() 的交点可由
的交点可由
求得交点为(1,1)和(4,4),此时![]() 在区间[1,4]上图象在直线y=x的下面,即
在区间[1,4]上图象在直线y=x的下面,即![]() 恒成立,所以m的最大值为4。
恒成立,所以m的最大值为4。
(2)设曲线上关于直线y=x的对称点为A(![]() )和B(
)和B(![]() ),线段AB的中点M(
),线段AB的中点M(![]() ),直线AB的方程为:
),直线AB的方程为:![]()

![]() (1分)
(1分)
![]()
又因为AB中点在直线y=x上,所以![]()
得![]() 9分
9分
(3)设P的坐标为![]() ,过P的切线方程为:
,过P的切线方程为:![]() ,则有
,则有

![]()
直线![]() 的两根,
的两根,
则![]() 14分
14分

练习册系列答案
相关题目
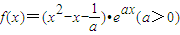
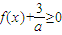 对任意的x∈R恒成立,求a的取值范围.
对任意的x∈R恒成立,求a的取值范围.
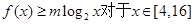 恒成立,求m的取值范围
恒成立,求m的取值范围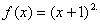
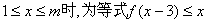 恒成立,求实数m的最大值;
恒成立,求实数m的最大值;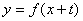 上存在两点关于直线
上存在两点关于直线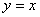 对称,求t的取值范围;
对称,求t的取值范围;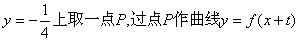 的两条切线l1、l2,求证:l1⊥l2
的两条切线l1、l2,求证:l1⊥l2