题目内容
 如图,已知半圆的直径|AB|=20,l为半圆外一直线,且与BA的延长线交于点T,|AT|=4,半圆上相异两点M、N与直线l的距离|MP|、|NQ|满足条件
如图,已知半圆的直径|AB|=20,l为半圆外一直线,且与BA的延长线交于点T,|AT|=4,半圆上相异两点M、N与直线l的距离|MP|、|NQ|满足条件 ,则|AM|+|AN|的值为
,则|AM|+|AN|的值为
- A.22
- B.20
- C.18
- D.16
B
分析:先以AT的中点O为坐标原点,AT的中垂线为y轴,可得半圆方程为(x-12)2+y2=100,根据条件得出M,N在以A为焦点,PT为准线的抛物线上,联立半圆方程和抛物线方程结合根与系数的关系,利用抛物线的定义即可求得答案.
解答: 解:以AT的中点O为坐标原点,AT的中垂线为y轴,
解:以AT的中点O为坐标原点,AT的中垂线为y轴,
可得半圆方程为(x-12)2+y2=100
又 ,设M(x1,y1),N(x2,y2),
,设M(x1,y1),N(x2,y2),
M,N在以A为焦点,PT为准线的抛物线上;以AT的垂直平分线为y轴,TA方向为x轴建立坐标系,则有
抛物线方程为y2=8x(y≥0),联立半圆方程和抛物线方程,
消去y得:x2-16x+44=0
∴x1+x2=16,
|AM|+|AN|=|MP|+|NQ|=x1+x2+4=20.
故选B.
点评:本小题主要考查抛物线的定义、圆的方程、圆与圆锥曲线的综合等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
分析:先以AT的中点O为坐标原点,AT的中垂线为y轴,可得半圆方程为(x-12)2+y2=100,根据条件得出M,N在以A为焦点,PT为准线的抛物线上,联立半圆方程和抛物线方程结合根与系数的关系,利用抛物线的定义即可求得答案.
解答:
 解:以AT的中点O为坐标原点,AT的中垂线为y轴,
解:以AT的中点O为坐标原点,AT的中垂线为y轴,可得半圆方程为(x-12)2+y2=100
又
 ,设M(x1,y1),N(x2,y2),
,设M(x1,y1),N(x2,y2),M,N在以A为焦点,PT为准线的抛物线上;以AT的垂直平分线为y轴,TA方向为x轴建立坐标系,则有
抛物线方程为y2=8x(y≥0),联立半圆方程和抛物线方程,
消去y得:x2-16x+44=0
∴x1+x2=16,
|AM|+|AN|=|MP|+|NQ|=x1+x2+4=20.
故选B.
点评:本小题主要考查抛物线的定义、圆的方程、圆与圆锥曲线的综合等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
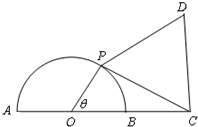 如图,已知⊙O的半径为1,点C在直径AB的延长线上,BC=1,点P是半圆上的一个动点,以PC为边作正三角形PCD,且点D与圆心分别在PC两侧.
如图,已知⊙O的半径为1,点C在直径AB的延长线上,BC=1,点P是半圆上的一个动点,以PC为边作正三角形PCD,且点D与圆心分别在PC两侧. 选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. (2012•黄冈模拟)(选做题:请在下列两题中任选一题作答,如果多做,则按所做的第一题评分)
(2012•黄冈模拟)(选做题:请在下列两题中任选一题作答,如果多做,则按所做的第一题评分) 从A,B,C,D四个中选做2个A.选修4-1(几何证明选讲)
从A,B,C,D四个中选做2个A.选修4-1(几何证明选讲)