题目内容
已知函数f(x)=alnx-ax-3(a∈R).
(1)求函数f(x)的单调区间;
(2)函数y=f(x)的图象在x=4处的切线的斜率为 ,若函数g(x)=
,若函数g(x)= x3+x2[f′(x)+
x3+x2[f′(x)+ ]在区间(1,3)上不是单调函数,求m的取值范围.
]在区间(1,3)上不是单调函数,求m的取值范围.
解 (1)f′(x)= (x>0),
(x>0),
①当a>0时,若x∈(0,1),则f′(x)>0;若x∈(1,+∞),则f′(x)<0,
∴当a>0时,f(x)的单调递增区间为(0,1],单调递减区间为[1,+∞);
②当a<0时,若x∈(1,+∞),则f′(x)>0;若x∈(0,1),则f′(x)<0,
∴当a<0时,f(x)的单调递增区间为[1,+∞),单调递减区间为(0,1];
③当a=0时,f(x)=-3,f(x)不是单调函数,无单调区间.
(2)由题意知,f′(4)=-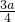 =
= ,得a=-2,则f(x)=-2lnx+2x-3,
,得a=-2,则f(x)=-2lnx+2x-3,
∴g(x)=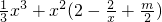 =
= x3+(
x3+( +2)x2-2x,
+2)x2-2x,
∴g′(x)=x2+(m+4)x-2.
∵g(x)在区间(1,3)上不是单调函数,且g′(0)=-2<0,
∴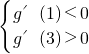 ,即
,即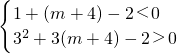 解得
解得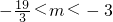 .
.
故m的取值范围是(- ,-3).
,-3).
分析:(1)求导数f′(x),利用导数与函数单调性的关系分情况讨论即可.
(2)由切线斜率为 ,可求出a值,进而求出f(x)、f′(x),因为g(x)在区间(1,3)上不单调,所以g′(x)改变符号,从而得到m所满足的条件.
,可求出a值,进而求出f(x)、f′(x),因为g(x)在区间(1,3)上不单调,所以g′(x)改变符号,从而得到m所满足的条件.
点评:本题考查了导数与函数单调性的关系,利用导数解决问题的能力,注意数形结合思想的应用.
 (x>0),
(x>0),①当a>0时,若x∈(0,1),则f′(x)>0;若x∈(1,+∞),则f′(x)<0,
∴当a>0时,f(x)的单调递增区间为(0,1],单调递减区间为[1,+∞);
②当a<0时,若x∈(1,+∞),则f′(x)>0;若x∈(0,1),则f′(x)<0,
∴当a<0时,f(x)的单调递增区间为[1,+∞),单调递减区间为(0,1];
③当a=0时,f(x)=-3,f(x)不是单调函数,无单调区间.
(2)由题意知,f′(4)=-
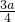 =
= ,得a=-2,则f(x)=-2lnx+2x-3,
,得a=-2,则f(x)=-2lnx+2x-3,∴g(x)=
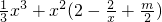 =
= x3+(
x3+( +2)x2-2x,
+2)x2-2x,∴g′(x)=x2+(m+4)x-2.
∵g(x)在区间(1,3)上不是单调函数,且g′(0)=-2<0,
∴
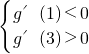 ,即
,即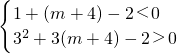 解得
解得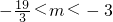 .
.故m的取值范围是(-
 ,-3).
,-3).分析:(1)求导数f′(x),利用导数与函数单调性的关系分情况讨论即可.
(2)由切线斜率为
 ,可求出a值,进而求出f(x)、f′(x),因为g(x)在区间(1,3)上不单调,所以g′(x)改变符号,从而得到m所满足的条件.
,可求出a值,进而求出f(x)、f′(x),因为g(x)在区间(1,3)上不单调,所以g′(x)改变符号,从而得到m所满足的条件.点评:本题考查了导数与函数单调性的关系,利用导数解决问题的能力,注意数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目