题目内容

已知正项等差数列{an}的前n项和为Sn，且满足，S7=56．
（Ⅰ）求数列{an}的通项公式an；
（Ⅱ）若数列{bn}满足b1=a1且bn+1-bn=an+1，求数列的前n项和Tn．

解：(Ⅰ) ∵{an}是等差数列且a1+a5=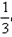a32，∴2a3=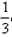a32，
又∵an＞0∴a3=6
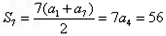∵∴a4=8
∴d=a4-a3=2，∴an=a3+(n-3)d=2n．
（Ⅱ）∵bn+1-bn=an+1且an=2n，∴bn+1-bn=2(n+1)
当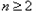时，，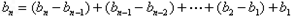
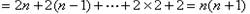当n=1时，b1=2满足上式，bn=n(n+1)
∴    
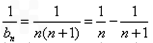
∴Tn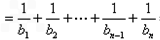
=
=．  

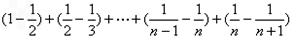
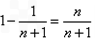练习册系列答案
相关题目
已知正项等差数列{an}的前20项和为100，则a5•a16的最大值是（　　）
A、100B、75C、25D、50
已知正项等差数列{an}的前20项的和为100，那么a7a14的最大值为（　　）
A、75B、100C、50D、25
已知非零向量
OA
、
OB
、
OC
、
OD
满足：
OA
=α
OB
+β
OC
+γ
OD
(α，β，γ∈R)，B、C、D为不共线三点，给出下列命题：
①若α=
3
2
，β=
1
2
，γ=-1，则A、B、C、D四点在同一平面上；
②当α＞0，β＞0，γ=
2
时，若|
OA
|=
3
，|
OB
|=|
OC
|=|
OD
|=1，＜
OB
，
OC
＞=
5π
6
，＜
OD
，
OB
＞=＜
OD
，
OC
＞=
π
2
，则α+β的最大值为
6
-
2
；
③已知正项等差数列an（n∈N*），若α=a2，β=a2009，γ=0，且A、B、C三点共线，但O点不在直线BC上，则
1
a3
+
4
a2008
的最小值为9；
④若α+β=1（αβ≠0），γ=0，则A、B、C三点共线且A分
BC
所成的比λ一定为
α
β
．
其中你认为正确的所有命题的序号是
 
．
已知正项等差数列{an}的前n项和为Sn，其中都是数列{an}中满足ah-ak=ak-am的任意项．
（I）证明：m+h=2k；
（II）证明：Sm•Sh≤Sk2；
（III）若
Sm
、
Sk
、
Sh
也在等差数列，且a1=a，求数列的前n项和．
（2011•成都一模）已知非零向量
OA
、
OB
、
OC
、
OD
满足：
OA
=α
OB
Z+β
OC
Z+γ
OD
Z（α，β，γ∈R），B、C、D为不共线三点，给出下列命题：
①若α=
3
2
，β=
1
2
，γ=-1，则A、B、C、D四点在同一平面上；
②若α=β=γ=1，|
OB
Z|+|
OC
|+|
OD
|=1，＜
OB
，
OD
＞=＜
OC
，
OD
＞=
π
2
，＜
OB
，
OC
＞=
π
3
，则|
OA
|=2；
③已知正项等差数列{an}（n∈N*Z），若α=a2，β=a2009，γ=0，且A、B、C三点共线，但O点不在直线BC上，则
1
a3
+
4
a2008
的最小值为10；
④若α=
4
3
，β=-
1
3
Z，γ=0，则A、B、C三点共线且A分
BC
所成的比λ一定为-4
其中你认为正确的所有命题的序号是
①②
①②
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网