Question

（本小题满分12分）

如图，过抛物线y²＝2px (p＞0)焦点F的直线交抛物线于A、B两点，O为坐标原点，l为抛物线的准线，点D在l上。

（1）求证：“如果A、O、D三点共线，则直线DB与

x轴平行”；

（2）写出（1）中命题的逆命题，判断它是真命题还是

假命题，并说明理由.

Answer 1

（1）证明：设点A的坐标为（，y₀），则直线OA的方程为

 （y₀≠0）   ①   抛物线的准线方程是x＝－             ②

联立①②，可得点D的纵坐标为y＝－             ③             （3分）

因为点F的坐标是（，0），所以直线AF的方程为y＝(x－)    ④

其中y≠p².联立y²＝2px与④，可得点B的纵坐标为y＝－             ⑤

由③⑤可知，DB∥x轴.                                           

当y＝p²时，结论显然成立.所以，直线DB平行于抛物线的对称轴.

（6分）

（2）逆命题：如果DB与x轴平行，则A、O、D三点共线它是真命题，证明如下

（8分）

因为抛物线y²＝2px（p＞0）的焦点为F（，0），所以经过点F的直线AB的方程可设为x＝my＋.代入抛物线方程，得y²－2pmy－p²＝0.

若记A（x₁，y₁），B（x₂，y₂），则y₁，y₂是该方程的两个根，所以y₁y₂＝－p².

（10分）

因为DB∥x轴，且点D在准线x＝－上，所以点D的坐标为（－，y₂），故直线DO的斜率为k＝，

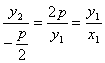即k也是直线OA的斜率，所以直线AD经过原点O，即A、O、D三点共线.

（12分）