题目内容
函数
，则f[f（3）]= ．
【答案】分析：由函数的解析式先求出f（3）的值，再求f[f（3）]的值．
解答：解：∵函数
，∴f（3）=7-2×3=1，
故有 f[f（3）]=f（1）=2+1=3，
故答案为 3．
点评：本题主要考查集合关系中参数的取值范围问题，体现了分类讨论的数学思想，属于基础题．
解答：解：∵函数
，∴f（3）=7-2×3=1，故有 f[f（3）]=f（1）=2+1=3，
故答案为 3．
点评：本题主要考查集合关系中参数的取值范围问题，体现了分类讨论的数学思想，属于基础题．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
函数f（x）的图象如图所示，f'（x）是函数f（x）的导函数，则下列排序正确的是（ ）| A、f'（3）＜f'（1）＜f（3）-f（1）＜0 | ||
B、f′(3)＜f′(1)＜
| ||
C、f′(1)＜
| ||
| D、f'（3）＜f（3）-f（1）＜f'（1）＜0 |
，则f[f（-3）]= ．
，则f[f（-3）]的值为 ．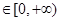
时f(x)是增函数，则f(-2),f(
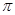),f(-3)的大小关系是：（ ）