题目内容
已知x>0,函数f(x)=-x2+2x+t-1,g(x)=x+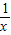 .
.(1)求过点(1,f(1))与y=f(x)图象相切的直线方程
(2)若g(x)=m有零点,求m的取值范围;
(3)确定实数t的取值范围,使得g(x)-f(x)=0有两个相异实根.
【答案】分析:(1)利用导数的几何意义即可得出切线的斜率f′(1),再利用点斜式即可得到切线的方程;
(2)利用导数得到g(x)的极小值即最小值,g(x)=m有零点?m≥g(x)min;
(3)令h(x)=g(x)-f(x),利用导数得出其最小值,g(x)-f(x)=0有两个相异实根?h(x)min<0.
解答:解:(1)∵f′(x)=-2x+2,∴f′(1)=0.
而f(1)=-1+2+t-1=t,
∴过点(1,f(1))与y=f(x)图象相切的直线方程是y-t=0.
(2)由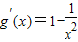 =
= ,x>0,令g′(x)=0,解得x=1.
,x>0,令g′(x)=0,解得x=1.
解g′(x)>0,得x>1,可得g(x)在(1,+∞)上单调递增;解g′(x)<0,得0<x<1,可得g(x)在(0,1)上单调递减.
因此当x=1时,g(x)取得极小值即最小值,g(1)=2,
∵g(x)=m有零点,∴m的取值范围是[2,+∞);
(3)令h(x)=g(x)-f(x)=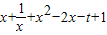 =
=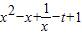 (x>0),
(x>0),
则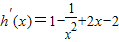 =
=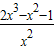 =
=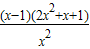 ,
,
令h′(x)=0,解得x=1.
解h′(x)>0,得x>1,可得h(x)在(1,+∞)上单调递增;解h′(x)<0,得0<x<1,可得h(x)在(0,1)上单调递减.
因此当x=1时,函数h(x)取得最小值,h(1)=2-t,
又x→0+时,h(x)→+∞;当x→+∞时,h(x)→+∞.
因此当h(1)<0,即t>2时,h(x)在x>0时与x轴由两个交点,即g(x)-f(x)=0有两个相异实根.
点评:本题考查了利用导数研究函数的单调性、极值与最值、导数的几何意义、函数的零点与方程的根等价转化等基础知识与基本技能,考查了推理能力和计算能力.
(2)利用导数得到g(x)的极小值即最小值,g(x)=m有零点?m≥g(x)min;
(3)令h(x)=g(x)-f(x),利用导数得出其最小值,g(x)-f(x)=0有两个相异实根?h(x)min<0.
解答:解:(1)∵f′(x)=-2x+2,∴f′(1)=0.
而f(1)=-1+2+t-1=t,
∴过点(1,f(1))与y=f(x)图象相切的直线方程是y-t=0.
(2)由
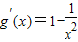 =
= ,x>0,令g′(x)=0,解得x=1.
,x>0,令g′(x)=0,解得x=1.解g′(x)>0,得x>1,可得g(x)在(1,+∞)上单调递增;解g′(x)<0,得0<x<1,可得g(x)在(0,1)上单调递减.
因此当x=1时,g(x)取得极小值即最小值,g(1)=2,
∵g(x)=m有零点,∴m的取值范围是[2,+∞);
(3)令h(x)=g(x)-f(x)=
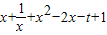 =
=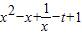 (x>0),
(x>0),则
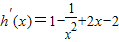 =
=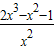 =
=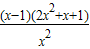 ,
,令h′(x)=0,解得x=1.
解h′(x)>0,得x>1,可得h(x)在(1,+∞)上单调递增;解h′(x)<0,得0<x<1,可得h(x)在(0,1)上单调递减.
因此当x=1时,函数h(x)取得最小值,h(1)=2-t,
又x→0+时,h(x)→+∞;当x→+∞时,h(x)→+∞.
因此当h(1)<0,即t>2时,h(x)在x>0时与x轴由两个交点,即g(x)-f(x)=0有两个相异实根.
点评:本题考查了利用导数研究函数的单调性、极值与最值、导数的几何意义、函数的零点与方程的根等价转化等基础知识与基本技能,考查了推理能力和计算能力.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 ,求f(x-1).
,求f(x-1). ,求f(x).
,求f(x). ,求f(x).
,求f(x).