题目内容
直线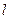 是双曲线
是双曲线 的右准线,以原点O为圆心且过双曲线焦点的圆被直线
的右准线,以原点O为圆心且过双曲线焦点的圆被直线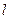 分成弧长为2:1的两段,则双曲线的离心率为
分成弧长为2:1的两段,则双曲线的离心率为
A. | B. | C. | D. |
A
解析

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
若抛物线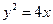 的焦点是
的焦点是 ,准线是
,准线是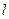 ,点
,点 是抛物线上一点,则经过点
是抛物线上一点,则经过点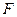 、
、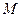 且与
且与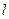 相切的圆共有 ( ).
相切的圆共有 ( ).
A.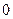 个 个 | B. 个 个 | C.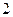 个 个 | D.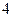 个 个 |
若椭圆两准线间的距离是焦距的4倍,则该椭圆的离心率为( )
A.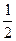 | B.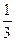 | C.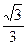 | D.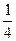 |
(10)设O为坐标原点,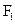 ,
,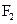 是双曲线
是双曲线 (a>0,b>0)的焦点,若在双曲线上存在点P,满足∠
(a>0,b>0)的焦点,若在双曲线上存在点P,满足∠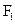 P
P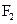 =60°,∣OP∣=
=60°,∣OP∣=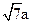 ,则该双曲线的渐近线方程为
,则该双曲线的渐近线方程为
A.x±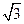 y="0" y="0" | B.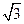 x±y=0 x±y=0 |
C.x±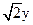 ="0" ="0" | D.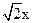 ±y=0 ±y=0 |
在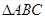 中,
中,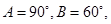 一椭圆与一双曲线都以
一椭圆与一双曲线都以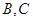 为焦点,且都过
为焦点,且都过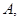 它们的离心率分别为
它们的离心率分别为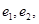 则
则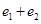 的值为( )
的值为( )
A.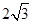 | B.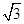 | C.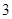 | D.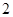 |
如图,用与底面成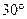 角的平面截圆柱得一椭圆截线,则该椭圆的离心率为 ( )
角的平面截圆柱得一椭圆截线,则该椭圆的离心率为 ( )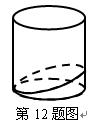
A.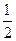 | B.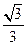 | C. | D.非上述结论 |
设抛物线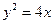 的准线与
的准线与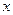 轴交于
轴交于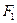 ,焦点为
,焦点为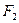 ,以
,以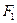 ,
,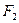 为焦点,离心率为
为焦点,离心率为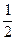 的椭圆的两条准线之间的距离为 ( )
的椭圆的两条准线之间的距离为 ( )
| A.4 | B.6 | C.8 | D.10 |
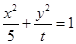 恒有公共点,则t的取值范围是 .
恒有公共点,则t的取值范围是 . 的左右顶点分别为M,N,P为椭圆上任意一点,且直线PM的斜率取值范围是
的左右顶点分别为M,N,P为椭圆上任意一点,且直线PM的斜率取值范围是 ,则直线PN的斜率的取值范围是
,则直线PN的斜率的取值范围是


