题目内容
已知数列{an}满足a1=1,an=2an-1+1,则an= .
【答案】分析:由已知变形可得数列{an+1}为公比为2的等比数列,又可得数列的首项,可得通项,移项可得所求.
解答:解:由an=2an-1+1可得an+1=2an-1+2=2(an-1+1),
故可得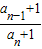 =2,故数列{an+1}为公比为2的等比数列,
=2,故数列{an+1}为公比为2的等比数列,
由题意可得该数列的首项为:a1+1=2,
故可得an+1=2×2n-1,故an=2n-1,
故答案为:2n-1
点评:本题考查等比关系的确定,由题意构造数列为等比数列并利用其通项公式是解决问题的关键,属中档题.
解答:解:由an=2an-1+1可得an+1=2an-1+2=2(an-1+1),
故可得
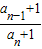 =2,故数列{an+1}为公比为2的等比数列,
=2,故数列{an+1}为公比为2的等比数列,由题意可得该数列的首项为:a1+1=2,
故可得an+1=2×2n-1,故an=2n-1,
故答案为:2n-1
点评:本题考查等比关系的确定,由题意构造数列为等比数列并利用其通项公式是解决问题的关键,属中档题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目