题目内容

已知椭圆
x2
9
+
y2
4
=1的焦点坐标为（　　）
A、(±
13
，0)
B、（±3，0）
C、(±
5
，0)
D、（±2，0）
分析：由椭圆的标准方程可知，其焦点在x轴，从而可得其焦点坐标．
解答：解：∵椭圆的标准方程为
x2
9
+
y2
4
=1，
∴a2=9，b2=4，
∴c2=a2-b2=5，且焦点在x轴，
∴椭圆
x2
9
+
y2
4
=1的焦点坐标为：（±
5
，0），
故选：C．
点评：本题考查椭圆的简单性质，考查椭圆的标准方程，属于基础题．
练习册系列答案
相关题目
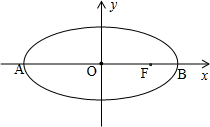精英家教网在平面直角坐标系xoy中，如图，已知椭圆
x2
9
+
y2
5
=1的左、右顶点为A、B，右焦点为F．设过点T（t，m）的直线TA、TB与椭圆分别交于点M（x1，y1）、N（x2，y2），其中m＞0，y1＞0，y2＜0．
（1）设动点P满足PF2-PB2=4，求点P的轨迹；
（2）设x1=2，x2=
1
3
，求点T的坐标；
（3）设t=9，求证：直线MN必过x轴上的一定点（其坐标与m无关）．
已知椭圆
x2
9
+y2=1，过左焦点F1倾斜角为
π
6
的直线交椭圆于A、B两点．求弦AB的长
2
2
．
已知椭圆
x2
9
+y2=1的两个焦点分别为F1，F2，点P在椭圆上且
PF1
•
PF2
=0，则△PF1F2的面积是（　　）
A、
1
2
B、
3
2
C、
3
3
D、1
已知椭圆
x2
9
+
y2
4
=1与双曲线
x2
4
-y2=1有共同焦点F1，F2，点P是两曲线的一个交点，则|PF1|•|PF2|=
5
5
．
已知椭圆
x2
9
+y2=1的两个焦点分别为F1，F2，点P在椭圆上且
PF1
•
PF2
=0，则△PF1F2的面积是（　　）
A．
1
2
B．
3
2
C．
3
3
D．1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网