题目内容
已知函数f(x)=Asin(2x+φ)(A>0,|φ|< ),且f(
),且f( )=-A.
)=-A.
(I)求φ的值;
(Ⅱ)若f(α)= ,f(β+
,f(β+ )=
)= 且
且 ,求cos(2α+2β-
,求cos(2α+2β- )的值.
)的值.
解:(I)由题意,得f( )=-A?Asin(2×
)=-A?Asin(2× +φ)=-A,
+φ)=-A,
∴sin( +φ)=-1,
+φ)=-1,
∴ +φ=2kπ+
+φ=2kπ+ ,k∈Z
,k∈Z
∵|φ|< ,
,
∴φ=- .
.
(Ⅱ)由(I)可知,函数f(x)=Asin(2x- ),
),
∵f(α)= ∴Asin(2α-
∴Asin(2α- )=
)= ,
,
∴sin(2α- )=
)= ,
,
又 ,
,
∴ ,
,
∴cos(2α- )=
)= ,
,
又f( )=
)= A,
A,
∴Asin(2β+ )=
)= ,
,
∴sin2β= ,
,
∵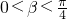 ,
,
∴ ,
,
∴cos2β= ,
,
∴cos(2α+2β- )=cos(2α-
)=cos(2α- )cos2β-sin(2α
)cos2β-sin(2α )sin2β
)sin2β
=
=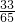 .
.
分析:(I)通过f( )=-A,结合|φ|<
)=-A,结合|φ|< 直接求出φ的值;
直接求出φ的值;
(Ⅱ)利用(I)求出函数的表达式,通过f(α)= ,求出sin(2α-
,求出sin(2α- ),cos(2α-
),cos(2α- ),利用f(β+
),利用f(β+ )=
)= 且
且 ,求出sin2β,cos2β的值,然后利用两角和的余弦函数求cos[(2α-
,求出sin2β,cos2β的值,然后利用两角和的余弦函数求cos[(2α- )+2β]的值.
)+2β]的值.
点评:本题是中档题,考查三角函数的解析式的求法,两角和与差的三角函数的应用,注意角的范围的转化,考查计算能力.
 )=-A?Asin(2×
)=-A?Asin(2× +φ)=-A,
+φ)=-A,∴sin(
 +φ)=-1,
+φ)=-1,∴
 +φ=2kπ+
+φ=2kπ+ ,k∈Z
,k∈Z∵|φ|<
 ,
,∴φ=-
 .
.(Ⅱ)由(I)可知,函数f(x)=Asin(2x-
 ),
),∵f(α)=
 ∴Asin(2α-
∴Asin(2α- )=
)= ,
,∴sin(2α-
 )=
)= ,
,又
 ,
,∴
 ,
,∴cos(2α-
 )=
)= ,
,又f(
 )=
)= A,
A,∴Asin(2β+
 )=
)= ,
,∴sin2β=
 ,
,∵
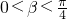 ,
,∴
 ,
,∴cos2β=
 ,
,∴cos(2α+2β-
 )=cos(2α-
)=cos(2α- )cos2β-sin(2α
)cos2β-sin(2α )sin2β
)sin2β=

=
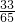 .
.分析:(I)通过f(
 )=-A,结合|φ|<
)=-A,结合|φ|< 直接求出φ的值;
直接求出φ的值;(Ⅱ)利用(I)求出函数的表达式,通过f(α)=
 ,求出sin(2α-
,求出sin(2α- ),cos(2α-
),cos(2α- ),利用f(β+
),利用f(β+ )=
)= 且
且 ,求出sin2β,cos2β的值,然后利用两角和的余弦函数求cos[(2α-
,求出sin2β,cos2β的值,然后利用两角和的余弦函数求cos[(2α- )+2β]的值.
)+2β]的值.点评:本题是中档题,考查三角函数的解析式的求法,两角和与差的三角函数的应用,注意角的范围的转化,考查计算能力.

练习册系列答案
相关题目