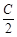题目内容

设a、b、c是三角形的三边长.求证:≥a+b+c.

证明:∵b+c-a＞0,∴+(b+c-a)≥2a,即有≥3a-b-c.

    同理,≥3b-c-a,≥3c-a-b.

    三式相加得证.

练习册系列答案
相关题目
设A、B、C是三角形的三个内角，下列关系恒成立的是（　　）
A、cos（A+B）=cosC
B、sin（A+B）=sinC
C、tan（A+B）=tanC
D、sin
A+B
2
=sin
C
2
设A，B，C是三角形的三边
（1）（文）若c=1，a，b是从{1，2，3，4，5，6}中任取的两个数（a，b可以相等），求a，b，c能构成三角形的概率；
（2）（文）若a，b是从（0，6）中任取的两个数（a，b可以相等），求构成以a为底边的等腰三角形的概率．
设a，b，c是三角形ABC的边长，对任意实数x，f（x）=b2x2+（b2+c2-a2）x+c2有（　　）
A、f（x）=0B、f（x）＞0C、f（x）≥0D、f（x）＜0
设A、B、C是三角形的三个内角，下列关系恒等成立的是(    )

A.cos(A+B)=cosC                B.sin(A+B)=sinC

C.tan(A+B)=tanC                D.sin=sin

．设A、B、C是三角形的三个内角，下列关系恒成立的是（ ）

A．cos（A+B）=cosC                       B．sin（A+B）=sinC

C．tan（A+B）=tanC                       D．sin=sin

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网