题目内容
【题目】已知两点A(0,﹣1),B(0,1),直线PA,PB相交于点P,且它们的斜率之积是![]() ,记点P轨迹为C.
,记点P轨迹为C.
(1)求曲线C的轨迹方程;
(2)直线l与曲线C交于M,N两点,若|AM|=|AN|,求直线l的斜率k的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)设![]() ,由
,由![]() 利用斜率公式,得到
利用斜率公式,得到![]() 关系式,整理即可求出结论;
关系式,整理即可求出结论;
(2)斜率![]() 显然成立,当
显然成立,当![]() 设直线
设直线![]() 方程为
方程为![]() 与椭圆方程联立,得到关于
与椭圆方程联立,得到关于![]() 的一元二次方程,由
的一元二次方程,由![]() ,得出关于
,得出关于![]() 的不等量关系,运用根与系数关系求出
的不等量关系,运用根与系数关系求出![]() 坐标关系,进而求出
坐标关系,进而求出![]() 中点
中点![]() 坐标,
坐标,![]() ,可得
,可得![]() ,求出
,求出![]() 关系,代入
关系,代入![]() 的不等量关系式,即可求出结论.
的不等量关系式,即可求出结论.
(1)设点P(x,y),则kPA![]() ,kPB
,kPB![]() ,
,
则有![]()
![]() ,整理得
,整理得![]() ,
,
即曲线C的轨迹方程为![]() ;
;
(2)当直线![]() 斜率不存在时,
斜率不存在时,![]() 显然不符,
显然不符,
故设直线![]() 方程为
方程为![]() ,代入
,代入![]() ,
,
整理得![]() ,
,
由已知条件可知![]() ,
,
即![]() ,①.
,①.
设![]() ,记
,记![]() 的中点为
的中点为![]() ,
,
则![]() ,
,
所以,![]() , ②
, ②
由![]() ,得
,得![]() ,所以
,所以![]() , ③
, ③
将②代入③化简得![]() ,即
,即![]() , ④
, ④
将④代入①得![]() ,即
,即![]() ,
,
得![]() 且
且![]() ,经检验,当
,经检验,当![]() 时,
时,![]() 也成立,
也成立,
故![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】某学生对其亲属30人的饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主).

(1)根据以上数据完成下列![]() 列联表:
列联表:
主食蔬菜 | 主食肉类 | 总计 | |
50岁以下 | |||
50岁以上 | |||
总计 |
(2)能否有99%的把握认为其亲属的饮食习惯与年龄有关?并写出简要分析.
参考公式和数据: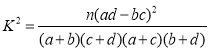 ,
,![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |