题目内容
已知函数y=ax2+bx+c的图象如图所示,则的值为( )
| A.2b | B.a-b+c |
| C.-2b | D.0 |
C
解析试题分析:根据题意,由于函数y=ax2+bx+c的图象可知开口向下,所以a<0,同时再y轴上的截距为正数,故可知c>0,那么可知f(1)=a+b+c,f(0)=c,f(-1)=0=a-b+c,a+c=b,可知二次函数对应的方程有两个根,那么结合条件,那么可知对称轴小于零,可知b<0,因此的值-2b ,故选C.
考点:二次函数的性质
点评:理解图像于性质之间的对应关系,主要是把握好对称轴的符号关系,以及开口即可,属于基础题。

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
已知函数 满足
满足 且
且 若对于任意的
若对于任意的 总有
总有 成立,则
成立,则 在
在 内的可能值有( )个
内的可能值有( )个
| A.1 | B.2 | C.3 | D.4 |
夏季高山上温度从山脚起每升高100米,降低0.7℃,已知山顶的温度是14.1℃,山脚的温度是26℃,则山的相对高度是( ) 米.
| A.1800 | B.1700 | C.1600 | D.1500 |
若点A(-1, ),B(0,
),B(0, ),C(4,
),C(4, )在二次函数
)在二次函数 (
( 为常数)的图像上,则
为常数)的图像上,则 ,
, ,
, 的大小关系为:
的大小关系为:
A. ﹤ ﹤ ﹤ ﹤ | B. ﹤ ﹤ ﹤ ﹤ | C. ﹤ ﹤ ﹤ ﹤ | D. ﹤ ﹤ ﹤ ﹤ |
已知 ,则
,则 的值为( )
的值为( )
A. | B. | C.1 | D.2 |
函数 的单调递增区间为( )
的单调递增区间为( )
A. | B. | C. | D. |
设函数 ,且
,且 恒成立,则对
恒成立,则对 ,下面不等式恒成立的是( )
,下面不等式恒成立的是( )
A. | B. | C. | D. |
设函数 若
若 ,则
,则 的取值范围是
的取值范围是
A. | B. | C. | D. |
 ,
, ,且
,且 ,当
,当 时,
时, ,
, ,
, ,则
,则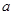 、
、 、
、 的大小顺序是( )。
的大小顺序是( )。 .
. 
 .
. 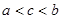
 .
. 
 .
. 