题目内容
已知函数 ,其中e为自然对数的底数,
,其中e为自然对数的底数,
(Ⅰ)当a=2时,求曲线y=f(x)在(1,f(1))处的切线与坐标轴围成的面积;
(Ⅱ)若函数f(x)存在一个极大值点和一个极小值点,且极大值与极小值的积为e5,求a的值。
 ,其中e为自然对数的底数,
,其中e为自然对数的底数,(Ⅰ)当a=2时,求曲线y=f(x)在(1,f(1))处的切线与坐标轴围成的面积;
(Ⅱ)若函数f(x)存在一个极大值点和一个极小值点,且极大值与极小值的积为e5,求a的值。
解:(Ⅰ)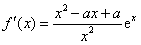 ,
,
当a=2时,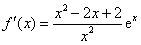 ,
,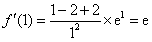 ,f(1)=-e,
,f(1)=-e,
所以曲线y=f(x)在(1,f(1))处的切线方程为y=ex-2e,
切线与x轴、y轴的交点坐标分别为(2,0),(0,-2e),
所以,所求面积为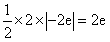 。
。
(Ⅱ)因为函数f(x)存在一个极大值点和一个极小值点,
所以,方程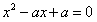 在(0,+∞)内存在两个不等实根,
在(0,+∞)内存在两个不等实根,
则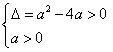 ,
,
所以a>4,
设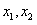 为函数f(x)的极大值点和极小值点,则
为函数f(x)的极大值点和极小值点,则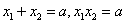 ,
,
因为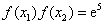 ,
,
所以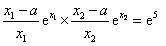 ,
,
即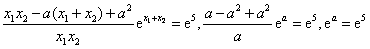 ,
,
解得:a=5,
此时f(x)有两个极值点,所以a=5。
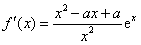 ,
,当a=2时,
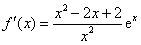 ,
,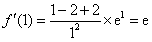 ,f(1)=-e,
,f(1)=-e,所以曲线y=f(x)在(1,f(1))处的切线方程为y=ex-2e,
切线与x轴、y轴的交点坐标分别为(2,0),(0,-2e),
所以,所求面积为
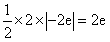 。
。(Ⅱ)因为函数f(x)存在一个极大值点和一个极小值点,
所以,方程
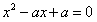 在(0,+∞)内存在两个不等实根,
在(0,+∞)内存在两个不等实根, 则
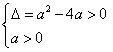 ,
, 所以a>4,
设
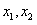 为函数f(x)的极大值点和极小值点,则
为函数f(x)的极大值点和极小值点,则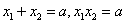 ,
,因为
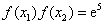 ,
,所以
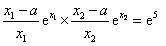 ,
,即
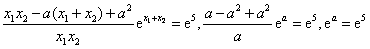 ,
,解得:a=5,
此时f(x)有两个极值点,所以a=5。

练习册系列答案
相关题目
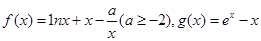 ,其中e为自然对数的底数,且当x>0时
,其中e为自然对数的底数,且当x>0时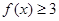 恒成立.
恒成立.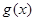 的单调区间;
的单调区间; .
. (其中e为自然对数)
(其中e为自然对数) 的极值。
的极值。 (常数a>0),当x>1时,求函数G(x)的单调区间,并在极值存在处求极值。
(常数a>0),当x>1时,求函数G(x)的单调区间,并在极值存在处求极值。 ,其中e为自然对数的底数.
,其中e为自然对数的底数.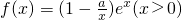 ,其中e为自然对数的底数.
,其中e为自然对数的底数. 在(1,l:x=1)处的切线与坐标轴围成的面积;
在(1,l:x=1)处的切线与坐标轴围成的面积;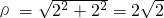 存在一个极大值点和一个极小值点,且极大值与极小值的积为e5,求a的值.
存在一个极大值点和一个极小值点,且极大值与极小值的积为e5,求a的值.