题目内容
（1）设a，b，c均为正实数，且a≠b≠c，求证：a3+b3＞a2b+ab2
（2）求证：
+2
＜2+
．
（2）求证：
| 3 |
| 2 |
| 7 |
（1）证明：（分析法）a3+b3＞a2b+ab2 成立，
只需证（a+b）（a2-ab+b2）＞ab（a+b）成立．
又因为a＞0，故只需证a2-ab+b2＞ab成立，
而依题设a≠b，则（a-b）2＞0显然成立，由此命题得证．
（2）证明：∵
+2
和2+
都是正数，
要证
+2
＜2+
只需证：(
+2
)2＜(2+
)2
整理得：11+2
＜11+2
即证：
＜
即证6＜7
∵6＜7 当然成立
∴原不等式成立．
只需证（a+b）（a2-ab+b2）＞ab（a+b）成立．
又因为a＞0，故只需证a2-ab+b2＞ab成立，
而依题设a≠b，则（a-b）2＞0显然成立，由此命题得证．
（2）证明：∵
| 3 |
| 2 |
| 7 |
要证
| 3 |
| 2 |
| 7 |
只需证：(
| 3 |
| 2 |
| 7 |
整理得：11+2
| 6 |
| 7 |
即证：
| 6 |
| 7 |
即证6＜7
∵6＜7 当然成立
∴原不等式成立．
练习册系列答案
相关题目
（选做题）在A，B，C，D四小题中只能选做2题，每小题10分，共计20分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．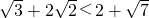
．
．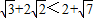