题目内容
(2013•湖北)在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5 ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
(1)求角A的大小;
(2)若△ABC的面积S=5
 ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.(1) (2)
(2)
 (2)
(2)
(1)由cos2A﹣3cos(B+C)=1,得2cos2A+3cosA﹣2=0,
即(2cosA﹣1)(cosA+2)=0,解得 (舍去).
(舍去).
因为0<A<π,所以 .
.
(2)由S= =
= =
= ,得到bc=20.又b=5,解得c=4.
,得到bc=20.又b=5,解得c=4.
由余弦定理得a2=b2+c2﹣2bccosA=25+16﹣20=21,故 .
.
又由正弦定理得 .
.
即(2cosA﹣1)(cosA+2)=0,解得
 (舍去).
(舍去).因为0<A<π,所以
 .
.(2)由S=
 =
= =
= ,得到bc=20.又b=5,解得c=4.
,得到bc=20.又b=5,解得c=4.由余弦定理得a2=b2+c2﹣2bccosA=25+16﹣20=21,故
 .
.又由正弦定理得
 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,acosA=bcosB.
,acosA=bcosB.
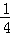 b2.
b2.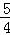 ,b=1时,求a,c的值;
,b=1时,求a,c的值; sin
sin  ,1),n=(cos
,1),n=(cos  ,求cos(
,求cos(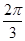 -α)的值;
-α)的值; ,试判断△ABC的形状.
,试判断△ABC的形状.
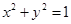 .已知时间
.已知时间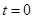 时,观光箱A的坐标为
时,观光箱A的坐标为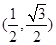 ,则当
,则当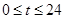 时(单位:分),动点A的纵坐标
时(单位:分),动点A的纵坐标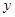 关于
关于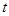 的函数的单调递减区间是 .
的函数的单调递减区间是 . ,那么b=
,那么b= B.
B. C.
C. D.
D.