题目内容
若集合A={x|x(2x-1)>0},B={y|y=log3(1-x)},则A∩B=
- A.∅
- B.

- C.

- D.
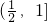
C
分析:解出集合A中x的取值范围,根据对数函数的定义求出x的范围,及有意义时值域求出y的范围,求A∩B即要求两个不等式的公共解集.
解答:由于x(2x-1)>0,解得:x> 或x<0,
或x<0,
所以集合A={x|x> 或x<0};
或x<0};
而由对数定义可知当1-x>0即x<1时,y取任意实数;
B=R;
则A∩B=(-∞,0)∪( ,1)
,1)
故选C
点评:考查学生掌握一元二次不等式的解法,会求对数函数的值域与最值,理解交集的定义并会利用交集进行运算.
分析:解出集合A中x的取值范围,根据对数函数的定义求出x的范围,及有意义时值域求出y的范围,求A∩B即要求两个不等式的公共解集.
解答:由于x(2x-1)>0,解得:x>
 或x<0,
或x<0,所以集合A={x|x>
 或x<0};
或x<0};而由对数定义可知当1-x>0即x<1时,y取任意实数;
B=R;
则A∩B=(-∞,0)∪(
 ,1)
,1)故选C
点评:考查学生掌握一元二次不等式的解法,会求对数函数的值域与最值,理解交集的定义并会利用交集进行运算.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目