题目内容
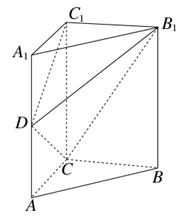
如图(1),在三角形ABC中,BA=BC=2√乏,ZABC=900,点0,M,N分别为线段的中点,将AABO和AMNC分别沿BO,MN折起,使平面ABO与平面CMN都与底面OMNB垂直,如图(2)所示.
(1)求证:AB//平面CMN;
(2)求平面ACN与平面CMN所成角的余
(3)求点M到平面ACN的距离.

(1)求证:AB//平面CMN;
(2)求平面ACN与平面CMN所成角的余
(3)求点M到平面ACN的距离.

详见解析
试题分析:(1)证明线与面平行,可通过证明线线平行,线面平行,或是面面平行,线面平行,此题很显然属于后者,根据已知,易证
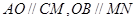 ,再根据线面与面面平行的判定定理证得;
,再根据线面与面面平行的判定定理证得;(2)这一问可通过空间向量,建立平面直角坐标系,易证
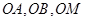 两两垂直,所以以
两两垂直,所以以 为原点建立空间直角坐标系,分别求出面
为原点建立空间直角坐标系,分别求出面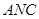 与面
与面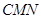 的法向量,利用公式
的法向量,利用公式 ,最后又 图像确定钝角还是锐角;
,最后又 图像确定钝角还是锐角;(3)在第二问的基础上,利用点到面的距离公式,
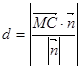 .此题比较容易,难点在求解法向量的计算过程容易出错,所以平时要加大法向量的求解要求.
.此题比较容易,难点在求解法向量的计算过程容易出错,所以平时要加大法向量的求解要求.试题解析:(1)
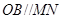 ,
,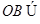 平面
平面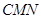
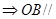 平面
平面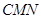
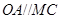 ,
,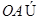 平面
平面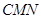
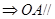 平面
平面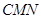
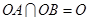 ,∴平面
,∴平面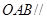 平面
平面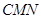 ,又
,又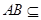 平面
平面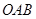 ,
,∴
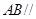 平面
平面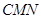 4分
4分(2)分别以
 为
为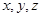 轴建立坐标系,
轴建立坐标系,则
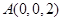 ,
, ,
,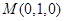 ,
, ,
,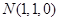 ,
,∴
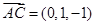 ,
,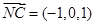 ,设平面
,设平面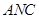 的法向量为
的法向量为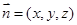 ,
,则有
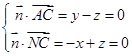 ,令
,令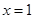 ,得
,得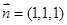 ,而平面
,而平面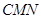 的法向量为:
的法向量为: ,
,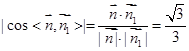 8分
8分(3)
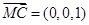 ,由(2)知平面
,由(2)知平面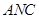 的法向量为:
的法向量为: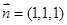 ,
,∴
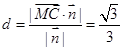 12分
12分
练习册系列答案
相关题目
 三点在球心为
三点在球心为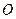 ,半径为
,半径为 的球面上,
的球面上,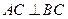 ,且
,且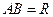 那么
那么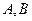 两点的球面距离为_______________,球心到平面
两点的球面距离为_______________,球心到平面 的距离为______________.
的距离为______________.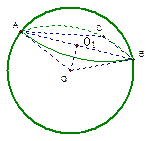
 两点间的距离为10,则
两点间的距离为10,则 __________.
__________.
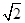
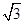
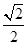
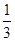 BD,AN=
BD,AN=