题目内容
已知函数![]() ,且
,且![]() 在(-∞,-1),(2,+∞)上单调递增,在(-1,2)上单调递减,又函数
在(-∞,-1),(2,+∞)上单调递增,在(-1,2)上单调递减,又函数![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)求证当![]() 时,
时,![]() ;
;
(Ⅲ)若函数![]() 的图象与函数
的图象与函数![]() 的图象共有3个交点,求
的图象共有3个交点,求![]() 的取值范围。
的取值范围。
解:(I)∵![]()
∴![]()
又函数![]() (―∞.―1).(2,+∞)上单调增。在(一1.2)上单调减
(―∞.―1).(2,+∞)上单调增。在(一1.2)上单调减
∴-1,2是方程![]() 的两个根
的两个根
从而 解得
解得 
∴![]()
(Ⅱ)令![]() =
=![]()
∴ ![]()
∵![]() ∴
∴![]()
从而函效![]() 在(4,+∞)上单调增
在(4,+∞)上单调增
又H(4)=0
∴当![]() 时
时![]()
(Ⅲ) ![]() 在(-∞,-1),(2,+∞)上单调增,在(-1,2)上单调 且
在(-∞,-1),(2,+∞)上单调增,在(-1,2)上单调 且![]() ,
,![]()
当![]() 时,直线
时,直线![]() 与函数
与函数![]() 的图象有3个交点.
的图象有3个交点.
又![]() ,且
,且![]()
∴当![]() 或
或![]() 时.直线
时.直线![]() 与
与![]() 的图象共有3个交点.
的图象共有3个交点.
综上:![]() 的取值范围是
的取值范围是![]()

练习册系列答案
相关题目
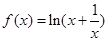 ,且
,且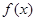 在
在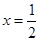 处的切线方程为
处的切线方程为 .
.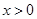 时,恒有
时,恒有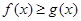 ;
;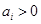 ,
,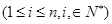 ,且
,且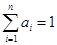 ,则
,则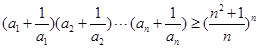 .
.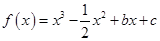 ,且
,且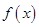 在
在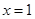 处取得极值.
处取得极值.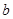 的值;
的值; 时,
时,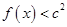 恒成立,求
恒成立,求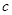 的取值范围;
的取值范围;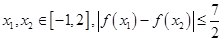 是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
是否恒成立?如果成立,给出证明,如果不成立,请说明理由.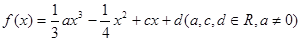 满足
满足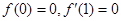 ,且
,且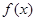 在
在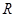 上单调递增.
上单调递增.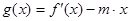 在区间
在区间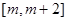 上的最小值为
上的最小值为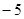 ,求实数
,求实数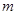 的值.
的值.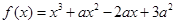 ,且在
,且在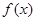 图象上点
图象上点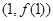 处的切线在y轴上的截距小于0,则a的取值范围是 ( )
处的切线在y轴上的截距小于0,则a的取值范围是 ( ) 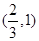 C.
C.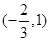 D.
D.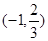
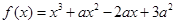 ,且在
,且在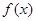 图象上点
图象上点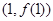 处的切线在y轴上的截距小于0,则a的取值范围是 ( )
处的切线在y轴上的截距小于0,则a的取值范围是 ( ) C.
C.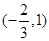 D.
D.