题目内容
老师告诉学生小明说,“若O为△ABC所在平面上的任意一点,且有等式
=
+λ(
+
),则P点的轨迹必过△ABC的垂心”,小明进一步思考何时P点的轨迹会通过△ABC的外心,得到的条件等式应为
=______.(用O,A,B,C四个点所构成的向量和角A,B,C的三角函数以及λ表示)
| OP |
| OA |
| ||
|
|
| ||
|
|
| OP |
由题意可得:
•(
+
)=-|
|+|
|=0
∴
与λ(
+
)垂直
设D为BC的中点,则
=
,
所以
=
+λ(
+
),即
=
+λ(
+
),
所以λ(
+
)=
,
因为
与λ(
+
)垂直
所以
•
=0,
又∵点D为BC的中点,
∴点P在BC的垂直平分线上,即P的轨迹会通过△ABC的外心.
故答案为:
=
+λ(
+
).
| BC |
| ||
|
|
| ||
|
|
| BC |
| BC |
∴
| BC |
| ||
|
|
| ||
|
|
设D为BC的中点,则
| ||||
| 2 |
| OD |
所以
| OP |
| ||||
| 2 |
| ||
|
|
| ||
|
|
| OP |
| OD |
| ||
|
|
| ||
|
|
所以λ(
| ||
|
|
| ||
|
|
| DP |
因为
| BC |
| ||
|
|
| ||
|
|
所以
| BC |
| DP |
又∵点D为BC的中点,
∴点P在BC的垂直平分线上,即P的轨迹会通过△ABC的外心.
故答案为:
| OP |
| ||||
| 2 |
| ||
|
|
| ||
|
|

练习册系列答案
相关题目
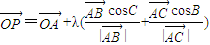 ,则P点的轨迹必过△ABC的垂心”,小明进一步思考何时P点的轨迹会通过△ABC的外心,得到的条件等式应为
,则P点的轨迹必过△ABC的垂心”,小明进一步思考何时P点的轨迹会通过△ABC的外心,得到的条件等式应为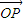 = .(用O,A,B,C四个点所构成的向量和角A,B,C的三角函数以及λ表示)
= .(用O,A,B,C四个点所构成的向量和角A,B,C的三角函数以及λ表示)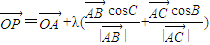 ,则P点的轨迹必过△ABC的垂心”,小明进一步思考何时P点的轨迹会通过△ABC的外心,得到的条件等式应为
,则P点的轨迹必过△ABC的垂心”,小明进一步思考何时P点的轨迹会通过△ABC的外心,得到的条件等式应为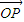 = .(用O,A,B,C四个点所构成的向量和角A,B,C的三角函数以及λ表示)
= .(用O,A,B,C四个点所构成的向量和角A,B,C的三角函数以及λ表示)